浙江省义乌市七校联考2018~2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-07-22 类型:期末考试
一、选择题(每小题3分,共30分)
-
1. 下列四个图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 某中学918班的8名同学在一次排球垫球测试中的成绩如下(单位:个):35、45、42、44、40、47、45、38,则这组数据的中位数和众数分别是( )A、42、47 B、41、45 C、42、45 D、43、453. 矩形具有而菱形不具有的性质是( )A、两组对边分别平行 B、对角线相等 C、两组对角分别相等 D、对角线互相垂直4. 用配方法解方程x2-2x-8=0,配方正确的是( )A、(x-1)2=7 B、(x-1)2=9 C、(x-1)2=-7 D、(x-1)2=35. 若点A(-3,y1),B(-2,y2),C(1,y3)都在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y2<y1<y3 B、y3<y1<y2 C、y1<y2<y3 D、y3<y2<y16. 若以A(-1,0),B(3,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 已知方程x2+mx+2=0的一个根是1,则它的另一个根是( )A、1 B、2 C、-2 D、-38. 一张四边形纸片剪去一个角后,内角和将( )A、减少180° B、不变 C、增加180° D、以上都有可能9. 已知平行四边形ABCD,对角线AC=6、BD=8,则该平行四边形四条边中最长边a的取值范围是( )A、 ≤a<7 B、5≤a<7 C、1<a<7 D、 ≤a<710. 已知正方形ABCD的边长为2,点E为正方形所在平面内一点,满足∠AED=90°,连接CE,若点F是CE的中点,则BF的最小值为( )
2. 某中学918班的8名同学在一次排球垫球测试中的成绩如下(单位:个):35、45、42、44、40、47、45、38,则这组数据的中位数和众数分别是( )A、42、47 B、41、45 C、42、45 D、43、453. 矩形具有而菱形不具有的性质是( )A、两组对边分别平行 B、对角线相等 C、两组对角分别相等 D、对角线互相垂直4. 用配方法解方程x2-2x-8=0,配方正确的是( )A、(x-1)2=7 B、(x-1)2=9 C、(x-1)2=-7 D、(x-1)2=35. 若点A(-3,y1),B(-2,y2),C(1,y3)都在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y2<y1<y3 B、y3<y1<y2 C、y1<y2<y3 D、y3<y2<y16. 若以A(-1,0),B(3,0),C(0,1)三点为顶点画平行四边形,则第四个顶点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 已知方程x2+mx+2=0的一个根是1,则它的另一个根是( )A、1 B、2 C、-2 D、-38. 一张四边形纸片剪去一个角后,内角和将( )A、减少180° B、不变 C、增加180° D、以上都有可能9. 已知平行四边形ABCD,对角线AC=6、BD=8,则该平行四边形四条边中最长边a的取值范围是( )A、 ≤a<7 B、5≤a<7 C、1<a<7 D、 ≤a<710. 已知正方形ABCD的边长为2,点E为正方形所在平面内一点,满足∠AED=90°,连接CE,若点F是CE的中点,则BF的最小值为( ) A、2 B、 -1 C、 D、2
A、2 B、 -1 C、 D、2二、填空题(每小题4分。共24分)
-
11. 若要使二次根式 -2在实数范围内有意义,则x的取值范围是 .
12. 用反证法证明“a>b”时,首先应该假设 .
13. 一个正n边形的一个外角等于72°,则n的值等于 .
14. 平行四边形ABCD的对角线AC与BD相交于点D,且AC⊥BD,请添加一个条件: , 使得平行四边形ABCD为正方形.
15. 某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图).若有43枚图钉可供选用,则最多可以按照要求展示绘画作品 张.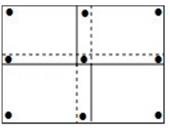
16. 如图1是一张可折叠的钢丝床的示意图,这是展开后支撑起来放在地面上的情况,如果折叠起来,床头部分被折到了床面之下(这里的A,B,C,D符点都是活动的),活动床头是根据三角形的稳定性和四边形的不稳定性设计而成的,其折叠过程可由图2的变换反映出来.如果已知四边形ABCD中,AB=6,CD=15,那么BC= ,AD=才能实现上述的折叠变化.
三、解答题(第17~19题每题6分,第20、21题每题8分,第22、23题10分,第24题12分,共66分)
-
17. 计算:(1)、(2)、18. 解方程:(1)、2x2-13x+1 5=0(2)、19. 如下图,每个长宽比为 :1的小格了4×4排列组成的方格纸,请你利用方格纸中的格点(每个小格子的顶点),画出两个n互不相等的正n边形(n≥3).
 20. 甲、乙两个汽车销售公司某年一至十月份每月销售同种品牌汽车的情况如下:(单位:辆)
20. 甲、乙两个汽车销售公司某年一至十月份每月销售同种品牌汽车的情况如下:(单位:辆)甲公司的各月销售数量分别为11,9,6,9,14,7,7,7,10,10.
乙公司的各月销售数量分别为3,4,5,8,12,8,8,13,1 3,16.
并绘制了如下折线统计图,请你从以下两个不同的方面对甲、乙两个汽车销售公司一至十月份的销售情况进行分析:
 (1)、已知甲公司甲均数是9,方差是5.2,请你求出乙公司的方差并回答哪个汽车销售公司的销售情况比较稳定.(2)、请你从甲、乙两个汽车销售公司销售数量的趋势分析,哪个汽车销售公司有较好的发展前景并简单说明理由.21. 如图,在△ABC中,D、F分别是BC、AC边的中点,连接DA、DF,且AD=2DF,过点B作AD的平行线交FD的延长线于点E.
(1)、已知甲公司甲均数是9,方差是5.2,请你求出乙公司的方差并回答哪个汽车销售公司的销售情况比较稳定.(2)、请你从甲、乙两个汽车销售公司销售数量的趋势分析,哪个汽车销售公司有较好的发展前景并简单说明理由.21. 如图,在△ABC中,D、F分别是BC、AC边的中点,连接DA、DF,且AD=2DF,过点B作AD的平行线交FD的延长线于点E. (1)、求证:四边形ABED为菱形;(2)、若BD=6,∠E=60°,求四边形ABEF的面积.22. 四川某特产专卖店销售核桃,其进价为每千克40元,按每千克60元销售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销量可增加20千克.若该专卖店销售这种核桃想要平均每天获利2240元,请回答:(1)、每千克核桃应降价多少元?(2)、在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折销售?(3)、若该专卖店打算每天获利至少2240元,请你直接写出每千克核桃售价m的取值范围 .23. 八年级数学兴趣小组组织了以“等积变形”为主题的课题研究.
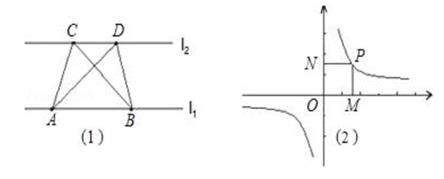
(1)、求证:四边形ABED为菱形;(2)、若BD=6,∠E=60°,求四边形ABEF的面积.22. 四川某特产专卖店销售核桃,其进价为每千克40元,按每千克60元销售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销量可增加20千克.若该专卖店销售这种核桃想要平均每天获利2240元,请回答:(1)、每千克核桃应降价多少元?(2)、在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折销售?(3)、若该专卖店打算每天获利至少2240元,请你直接写出每千克核桃售价m的取值范围 .23. 八年级数学兴趣小组组织了以“等积变形”为主题的课题研究.第一学习小组发现:如图(1),点A、点B在直线l1上,点C、点D在直线l2上,若l1∥l2 , 则S△ABC=S△ABD;反之亦成立.
第二学习小组发现:如图(2),点P是反比例函数y= 上任意一点,过点P作x轴、y轴的垂线,垂足为M,N,则矩形OMPN的面积为定值|k|.请利用上述结论解决下列问题:
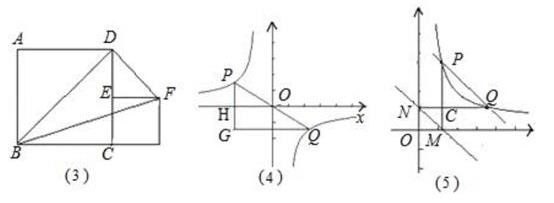 (1)、如图(3),四边形ABCD与四边形CEFG都是正方形,点E在CD上,正方形ABCD边长为2,则S△BDF= .
(1)、如图(3),四边形ABCD与四边形CEFG都是正方形,点E在CD上,正方形ABCD边长为2,则S△BDF= .
(2)、如图(4),点P、Q在反比例函数y= 图象上,PQ过点O,过P作y轴的平行线交x轴于点H,过Q作x轴的平行线交PH于点G,若S△PQG=8,则S△POH= , k= .
(3)、如图(5)点P、Q是第一象限的点,且在反比例函数y= 图象上,过点P作x轴垂线,过点P作y轴垂线,垂足分别是M、N,试判断直线PQ与直线MN的位置关系,并说明理由.
24. 如图,在平面直角坐标系中,O是原点,点A在x轴的负半轴上,点B在y轴的正半轴上,AO=2OB,且线段OB的长是方程x2-2x-8=0的一个根.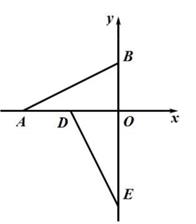 (1)、求直线AB的函数解析式.(2)、将△ABD绕点O逆时针方向旋转90°得到△EDO,直线ED交线段AB 于点C,点F是直线CE上一点,分别过点E、F作x轴和y轴的平行线交于点G,将△EFG沿EF折叠,使点G的对应点落在坐标轴上,求点F的坐标.(3)、在(2)的条件下,点M是DO中点,点N、P、Q在直线BD或者y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请利用备用图画出示意图并直接写出点P的坐标;若不存在,请说明理由.
(1)、求直线AB的函数解析式.(2)、将△ABD绕点O逆时针方向旋转90°得到△EDO,直线ED交线段AB 于点C,点F是直线CE上一点,分别过点E、F作x轴和y轴的平行线交于点G,将△EFG沿EF折叠,使点G的对应点落在坐标轴上,求点F的坐标.(3)、在(2)的条件下,点M是DO中点,点N、P、Q在直线BD或者y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请利用备用图画出示意图并直接写出点P的坐标;若不存在,请说明理由.