浙江省温州市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-07-22 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分.)
-
1. 在直角坐标系中,若点Q与点 P(2,3)关于原点对称,则点Q的坐标是( )A、(-2,3) B、(2,-3) C、(-2,-3) D、(-3,-2)2. 下列选项中的图形,不属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,矩形ABCD的对角线交于点O.若∠BAO=55°,则∠AOD等于( )
3. 如图,矩形ABCD的对角线交于点O.若∠BAO=55°,则∠AOD等于( )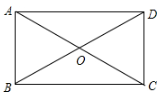 A、110° B、115° C、120° D、125°4. 下列选项中的计算,正确的是( )A、 =±3 B、2 - =2 C、 =-5 D、5. 如图,五边形ABCDE的每一个内角都相等,则外角∠CBF等于( )
A、110° B、115° C、120° D、125°4. 下列选项中的计算,正确的是( )A、 =±3 B、2 - =2 C、 =-5 D、5. 如图,五边形ABCDE的每一个内角都相等,则外角∠CBF等于( )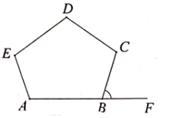 A、60° B、72° C、80° D、108°6. 人文书店三月份销售某畅销书100册,五月份销售量达196册,设月平均增长率为x,则可列方程( )A、100(1+x)=196 B、100(1+2x)=196 C、100(1+x2)=196 D、100(1+x)2=1967. 若关于x的方程x2+6x-a=0无实数根,则a的值可以是下列选项中的( )A、-10 B、-9 C、9 D、108. 已知点(-2,y1),(-1,y2),(4,y3)在函数y= 的图象上,则( )A、y2<y1<y3 B、y1<y2<y3 C、y3<y1<y2 D、y3<y2<y19. 如图,架在消防车上的云梯AB长为10m,∠ADB=90°,AD=2BD,云梯底部离地面的距离BC为2m,则云梯的顶端离地面的距离AE为( )
A、60° B、72° C、80° D、108°6. 人文书店三月份销售某畅销书100册,五月份销售量达196册,设月平均增长率为x,则可列方程( )A、100(1+x)=196 B、100(1+2x)=196 C、100(1+x2)=196 D、100(1+x)2=1967. 若关于x的方程x2+6x-a=0无实数根,则a的值可以是下列选项中的( )A、-10 B、-9 C、9 D、108. 已知点(-2,y1),(-1,y2),(4,y3)在函数y= 的图象上,则( )A、y2<y1<y3 B、y1<y2<y3 C、y3<y1<y2 D、y3<y2<y19. 如图,架在消防车上的云梯AB长为10m,∠ADB=90°,AD=2BD,云梯底部离地面的距离BC为2m,则云梯的顶端离地面的距离AE为( )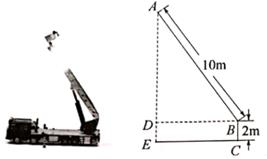 A、(2 +2)m B、(4 +2)m C、(5 +2)m D、7m10. 《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为 x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为( )
A、(2 +2)m B、(4 +2)m C、(5 +2)m D、7m10. 《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为 x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为( )
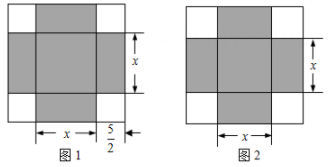 A、6 B、3 -3 C、3 -2 D、3
A、6 B、3 -3 C、3 -2 D、3二、填空题(本题有8小题,每小题3分,共24分)
-
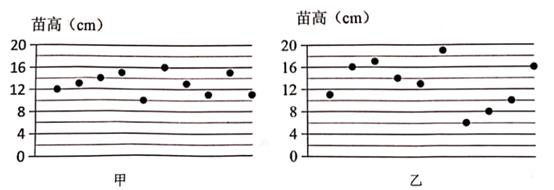
11. 要使二次根式 有意义,则a的取值范围是 .12. 用反证法证明“如果lal>a,那么a<0.”是真命题时,第一步应先假设 .13. 某水池容积为300m3 , 原有水100m3 , 现以xm3/min的速度匀速向水池中注水,注满水需要y min,则y关于x的函数表达式为 .14. 为了考察甲、乙两块地小麦的长势,分别从中随机抽出10株苗,测得苗高如图所示.若 和 分别表示甲、乙两块地苗高数据的方差,则 .(填“>”、“<”或“=”).
 15. 如图,在 ABCD中,∠A=45°,BC=2,则AB与CD之间的距离为 .
15. 如图,在 ABCD中,∠A=45°,BC=2,则AB与CD之间的距离为 .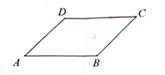 16. 用配方法解一元二次方程x2-mx=1时,可将原方程配方成(x-3)2=n,则m+n的值是 .17. 如图,将菱形纸片ABCD折叠,使点C,D的对应点C',D'都落在直线AB上,折痕为EF,若EF=6.AC'=8,则阴影部分(四边形ED'BF)的面积为 。
16. 用配方法解一元二次方程x2-mx=1时,可将原方程配方成(x-3)2=n,则m+n的值是 .17. 如图,将菱形纸片ABCD折叠,使点C,D的对应点C',D'都落在直线AB上,折痕为EF,若EF=6.AC'=8,则阴影部分(四边形ED'BF)的面积为 。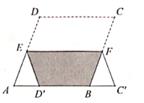 18. 如图,点A,B分别在x轴、y轴上,点O关于AB的对称点C在第一象限,将△ABC沿x轴正方向平移k个单位得到△DEF(点B与E是对应点),点F落在双曲线y= 上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 .
18. 如图,点A,B分别在x轴、y轴上,点O关于AB的对称点C在第一象限,将△ABC沿x轴正方向平移k个单位得到△DEF(点B与E是对应点),点F落在双曲线y= 上,连结BE交该双曲线于点G.∠BAO=60°,OA=2GE,则k的值为 .
三、解答题(本题有6小题,共46分.)
-
19.(1)、计算: .(2)、解方程:(x+2)2=9.20. 如图,在正方形方格纸中,线段AB的两个端点和点P都在小方格的格点上,分别按下列要求画格点四边形.
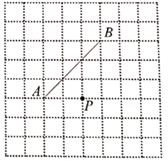 (1)、在图甲中画一个以AB为边的平行四边形,使点P落在AB的对边上(不包括端点).(2)、在图乙中画一个以AB为对角线的菱形,使点P落在菱形的内部(不包括边界).
(1)、在图甲中画一个以AB为边的平行四边形,使点P落在AB的对边上(不包括端点).(2)、在图乙中画一个以AB为对角线的菱形,使点P落在菱形的内部(不包括边界).(注:图甲、图乙在答卷纸上)
21. 在“2019慈善一日捐”活动中,某校八年级(1)班40名同学的捐款情况如下表:捐款金额(元)
20
30
50
a
80
100
人数(人)
2
8
16
x
4
7
根据表中提供的信息回答下列问题:
(1)、x的值为 ,捐款金额的众数为元,中位数为元.(2)、已知全班平均每人捐款57元,求a的值.22. 如图,矩形ABCD的边BC在x轴上,点A(a,4)和D分别在反比函数y= 和y= (m>0)的图象上.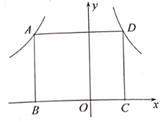 (1)、当AB=BC时,求m的值。(2)、连结OA,OD.当OD平分∠AOC时,求△AOD的周长.
(1)、当AB=BC时,求m的值。(2)、连结OA,OD.当OD平分∠AOC时,求△AOD的周长.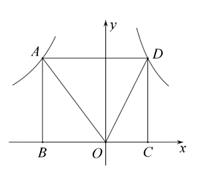 23. 阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).
23. 阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).
 (1)、求步道的宽.(2)、为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.已知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2 , 且区域丙为正方形,求塑胶跑道的总面积.24. 如图,点C在线段AB上,过点C作CD⊥AB,点E,F分别是AD,CD的中点,连结EF并延长EF至点G,使得FG=CB,连结CE,GB,过点B作BH∥CE交线段EG于点H.
(1)、求步道的宽.(2)、为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.已知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2 , 且区域丙为正方形,求塑胶跑道的总面积.24. 如图,点C在线段AB上,过点C作CD⊥AB,点E,F分别是AD,CD的中点,连结EF并延长EF至点G,使得FG=CB,连结CE,GB,过点B作BH∥CE交线段EG于点H.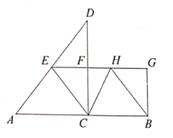
(1)、求证:四边形FCBG是矩形.(2)、已知AB=10, .①当四边形ECBH是菱形时,求EG的长.
②连结CH,DH,记△DEH的面积为S1 , △CBH的面积为S2 . 若EG=2FH,求S1+S2的值.