浙江省湖州市南浔区2018-2019年八年级下学期数学期末考试试卷
试卷更新日期：2019-07-22 类型：期末考试
一、选择题(本题有10小题，每小题3分，共30分)
-
1. 下列二次根式是最简二次根式的是（ ）A、 B、 C、 D、2. 下列汽车标志的图案中，是中心对称图形的是（ ）A、
B、
C、
D、
3. 为了考察甲、乙两块地小麦的长势，分别从中抽出10株苗，测出苗高，以下统计量中可以比较出两地长势哪一块更整齐的是（ ）A、平均数 B、中位数 C、方差 D、众数4. 用配方法解方程x2-3x-3=0时，配方结果正确的是（ ）A、(x-3)2=3 B、(x- )2=3 C、(x-3)2= D、(x- )2=5. 下列说法正确的是（ ）A、一组对边平行，另一组对边相等的四边形是平行四边形 B、对角线相等的平行四边形是菱形 C、三个角都是直角的四边形是矩形 D、一组邻边相等的平行四边形是正方形6. 某多边形的每个内角均为135°，则此多边形的边数为（ ）A、5 B、6 C、7 D、87. 若点A(1，y1)，B(-3，y2)在反比例函数y= (m≠0)的图象上，则y1 ， y2和0的大小关系是（ ）A、y1<0<y2 B、y1>0>y2 C、y1<y2<0 D、y1>y2>08. 用反证法证明命题“在同一平面内，如果两条直线都和第三条直线平行，那么这两条直线互相平行”，第一步应假设（ ）A、这两条直线互相垂直 B、这两条直线互相平行 C、这两条直线不平行 D、这两条直线不垂直9. 欧几里得的《几何原本》中记载了用图解法求解一元二次方程的方法，小南读了后，想到一个可以求解方程x2-bx+a2=0的图解方法：如图，在矩形ABCD(AB>BC)中，AB= ，BC=a，以A为圆心，作AE=AB，交DC于点E，则该方程的其中一个正根是（ ）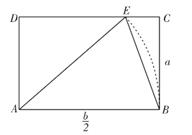
A、BE的长 B、CE的长 C、AB的长 D、AD的长10. 在数学课拓展课上，小明发现：若一条直线经过平行四边形对角线的交点，则这条直线平分该平行四边形的面积．如图是由5个边长是1，且一个内角是60°的小菱形拼成的图形，P是其中4个小菱形的公共顶点，小新在小明的启发下，将该图形沿着过点P的某条直线剪一刀，把它剪成了面积相等的两部分，则剪痕的长度是（ ）
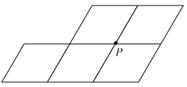A、2 B、3 C、 D、二、填空题(本题有6小题，每小题4分，共24分)
-
11. 若二次根式 有意义，则x的取值范围是 ．12. 数据1，2，3，4，6，3的众数是 ．13. 如图，A、B两处被池塘隔开，为了测量A、B两处的距离，在AB外选适当的点C，连结AC、BC，并分别取线段AC、BC的中点E、F，测得EF=22m，则AB=m．
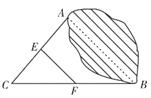14. 已知关于x的一元二次方程2x2-4x+c=0有两个相等的实数根，则c的值是 ．15. 如图，小浔用七巧板拼成一幅鸭子的装饰图，放入矩形ABCD内，装饰图中的正方形(4)顶点在边AD上，三角形(2)的斜边在边BC上，一顶点在顶点C处，三角形(5)中的斜边在AB上，记矩形ABCD内鸭子图案的面积为S1 ， 矩形ABCD的面积为S2 ， 则 的值是 ．
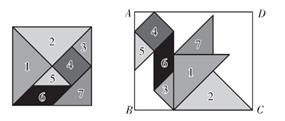16. 已知△ABC中，AB=AC=5，BC=6，D为平面内一点，若以A、B、C、D为顶点的四边形满足对角线互相垂直，且有一组对边相等，这个四边形的面积是 ．
三、解答题(本题有8小题，共66分)
-
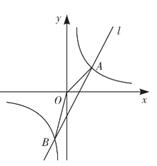
17. 计算：18. 解方程：x2-4x-1=0.19. 已知反比例函数y= 与直线l交于点A(2，2)和点B(-1，m)
(1)、 求k与m的值；(2)、 求△OAB的面积．20. 在学校组织的知识竞赛中，每班都选25人参加比赛，成绩分为A、B、C、D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，其中将90分及以上定为优秀分数，学校将八年级一班和二班的成绩整理并绘制如下的统计图．
请你根据以上提供的信息解答下列问题：
(1)、 补全两个统计图；(温馨提示：请画在答题卷相对应的图上)(2)、将下列表格补充完整．(温馨提示：请填写在答题卷相对应的表格内)班级 成绩
平均数（分）
中位数（分）
优秀率
一班
87.6
72%
二班
87.6
80
(3)、从以上信息进行分析，你认为哪个班更优秀?并说明理由．21. 如图，已知在矩形ABCD中，AB=8，AD=6，点E、F分别在边CD、AB上，且DE=BF．
(1)、 求证：四边形AFCE是平行四边形；(2)、若▱AFCE是菱形，求菱形AFCE的周长．22. 林场要建一个果园(如图矩形ABCD)，果园的一向靠墙(墙最大可用长度为25米)，另三边用木栏围成，在BC上开一个宽为1米的门(不用木栏)，小栏总长63米，计划建果园面积为440平方米．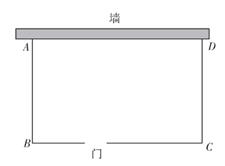
(1)、求AB的长；(2)、 现在准备在地面上为种植果树打一些面积固定的框，要求每个框的面积a不少于0.4平方米，但又不超过0.44平方米，请写出果园内打框的个数y关于a的解析式，并求出y的取值范围．23. 定义：有一组邻边相等，且它们的夹角为60°的四边形叫做半等边四边形．
(1)、已知在半等边四边形ABCD中，AB=AD，∠BAD=60°，∠BCD=120°．①如图1，若∠B=∠D，求证：BC=CD；
②如图2，连结AC，探索线段AC、BC、CD之间的数量关系，并说明理由；
(2)、如图3，已知∠MAC=30°，AC=10+10 ，点D是射线AM上的一个动点，记∠DCA=a，点B在直线AC的下方，若四边形ABCD是半等边四边形，且CB=CD．问：当点D在15°≤a≤45°的变化过程中运动时，点B也随之运动，请直接写出点B所经过的路径长．24. 如图1，在平面直角坐标系xOy中，已知△ABC，∠ABC=90°，顶点A在第一象限内，BC在x轴的正半轴上(B在C的右侧)，AB= ，∠ACB=30°，△ADC与△ABC关于AC所在的直线对称，且函数y= (k>0)的图象过点D．
(1)、当OC=2时，求k的值；(2)、如图2，若点A和点D在同一个反比例函数图象上，求OC的长；(3)、在(2)的条件下，点D与点E关于原点成中心对称，x轴上有一点F，平面内有一点G，若D、E、F、G四点构成的四边形是矩形，求F点的坐标．