湖北省十堰市2019年中考数学试卷
试卷更新日期:2019-07-22 类型:中考真卷
一、单选题
-
1. 下列实数中,是无理数的是( )A、 B、 C、 D、2. 如图,直线 ,直线 ,若 ,则 ( )
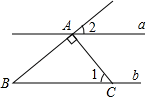 A、 B、 C、 D、3. 如图是一个 形状的物体,则它的俯视图是( )
A、 B、 C、 D、3. 如图是一个 形状的物体,则它的俯视图是( )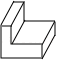 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 矩形具有而平行四边形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分6. 一次数学测试,某小组 名同学的成绩统计如下(有两个数据被遮盖):
4. 下列计算正确的是( )A、 B、 C、 D、5. 矩形具有而平行四边形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分6. 一次数学测试,某小组 名同学的成绩统计如下(有两个数据被遮盖):组员
甲
乙
丙
丁
戊
平均成绩
众数
得分
■
■
则被遮盖的两个数据依次是( )
A、 B、 C、 D、7. 十堰即将跨入高铁时代,钢轨铺设任务也将完成.现还有 米的钢轨需要铺设,为确保年底通车,如果实际施工时每天比原计划多铺设 米,就能提前 天完成任务.设原计划每天铺设钢轨 米,则根据题意所列的方程是( )A、 B、 C、 D、8. 如图,四边形 内接于⊙ , 交 的延长线于点 ,若 平分 , ,则 ( ) A、 B、 C、 D、9. 一列数按某规律排列如下: …,若第 个数为 ,则 ( )A、 B、 C、 D、10. 如图,平面直角坐标系中, ,反比例函数 的图象分别与线段 交于点 ,连接 .若点 关于 的对称点恰好在 上,则 ( )
A、 B、 C、 D、9. 一列数按某规律排列如下: …,若第 个数为 ,则 ( )A、 B、 C、 D、10. 如图,平面直角坐标系中, ,反比例函数 的图象分别与线段 交于点 ,连接 .若点 关于 的对称点恰好在 上,则 ( )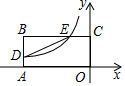 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
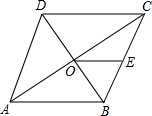
11. 如图,已知菱形 的对角线 交于点 为 的中点,若 ,则菱形的周长为.
 12. 我市“创建文明城市”活动正如火如荼的展开.某校为了做好“创文”活动的宣传,就本校学生对“创文”有关知识进行测试,然后随机抽取了部分学生的测试成绩进行统计分析,并将分析结果绘制成如下两幅不完整的统计图:
12. 我市“创建文明城市”活动正如火如荼的展开.某校为了做好“创文”活动的宣传,就本校学生对“创文”有关知识进行测试,然后随机抽取了部分学生的测试成绩进行统计分析,并将分析结果绘制成如下两幅不完整的统计图: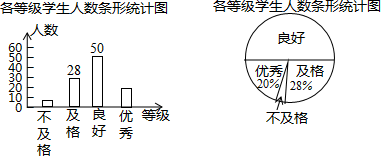
若该校有学生 人,请根据以上统计结果估计成绩为优秀和良好的学生共有人.
13. 对于实数 ,定义运算“◎”如下: ◎ .若 ◎ ,则 .14. 如图, 为半圆的直径,且 ,将半圆绕点 顺时针旋转 ,点 旋转到点 的位置,则图中阴影部分的面积为.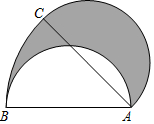 15. 如图,正方形 和 , ,连接 .若 绕点 旋转,当 最大时, .
15. 如图,正方形 和 , ,连接 .若 绕点 旋转,当 最大时, .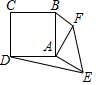
三、计算题
-
16. 计算: .17. 先化简,再求值: ,其中 .18. 如图,拦水坝的横断面为梯形 ,坝高 ,坡角 , ,求 的长.
 19. 第一盒中有 个白球、 个黄球,第二盒中有 个白球、 个黄球,这些球除颜色外无其他差别.(1)、若从第一盒中随机取出 个球,则取出的球是白球的概率是.(2)、若分别从每个盒中随机取出 个球,请用列表或画树状图的方法求取出的两个球中恰好 个白球、 个黄球的概率.20. 已知于 的元二次方程 有两个不相等的实数根 .(1)、求 的取值范围;(2)、若 x12+x22-x1x2≤30 ,且 为整数,求 的值.21. 如图, 中, ,以 为直径的⊙ 交 于点 ,点 为 延长线上一点,且 .
19. 第一盒中有 个白球、 个黄球,第二盒中有 个白球、 个黄球,这些球除颜色外无其他差别.(1)、若从第一盒中随机取出 个球,则取出的球是白球的概率是.(2)、若分别从每个盒中随机取出 个球,请用列表或画树状图的方法求取出的两个球中恰好 个白球、 个黄球的概率.20. 已知于 的元二次方程 有两个不相等的实数根 .(1)、求 的取值范围;(2)、若 x12+x22-x1x2≤30 ,且 为整数,求 的值.21. 如图, 中, ,以 为直径的⊙ 交 于点 ,点 为 延长线上一点,且 .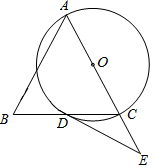 (1)、求证: 是⊙ 的切线;(2)、若 ,求⊙ 的半径.22. 某超市拟于中秋节前 天里销售某品牌月饼,其进价为 元/kg .设第x天的销售价格为 y(元/kg ),销售量为m(kg) .该超市根据以往的销售经验得出以下的销售规律:①当 时, ;当 时, 与 满足一次函数关系,且当 时, ; 时, .② 与 的关系为 .
(1)、求证: 是⊙ 的切线;(2)、若 ,求⊙ 的半径.22. 某超市拟于中秋节前 天里销售某品牌月饼,其进价为 元/kg .设第x天的销售价格为 y(元/kg ),销售量为m(kg) .该超市根据以往的销售经验得出以下的销售规律:①当 时, ;当 时, 与 满足一次函数关系,且当 时, ; 时, .② 与 的关系为 .
(1)、当 时, 与 的关系式为;
(2)、 为多少时,当天的销售利润 (元)最大?最大利润为多少?(3)、若超市希望第 天到第 天的日销售利润 (元)随 的增大而增大,则需要在当天销售价格的基础上涨 元/ ,求 的最小值.23. 如图1, 中, 为 内一点,将 绕点 按逆时针方向旋转角 得到 ,点 的对应点分别为点 ,且 三点在同一直线上. (1)、填空: (用含 的代数式表示);(2)、如图2,若 ,请补全图形,再过点 作 于点 ,然后探究线段 之间的数量关系,并证明你的结论;(3)、若 ,且点 满足 ,直接写出点 到 的距离.24. 已知抛物线 经过点 和 ,与 轴交于另一点 ,顶点为 .
(1)、填空: (用含 的代数式表示);(2)、如图2,若 ,请补全图形,再过点 作 于点 ,然后探究线段 之间的数量关系,并证明你的结论;(3)、若 ,且点 满足 ,直接写出点 到 的距离.24. 已知抛物线 经过点 和 ,与 轴交于另一点 ,顶点为 .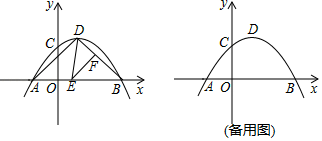 (1)、求抛物线的解析式,并写出 点的坐标;(2)、如图,点 分别在线段 上( 点不与 重合),且 ,则 能否为等腰三角形?若能,求出 的长;若不能,请说明理由;(3)、若点 在抛物线上,且 ,试确定满足条件的点 的个数.
(1)、求抛物线的解析式,并写出 点的坐标;(2)、如图,点 分别在线段 上( 点不与 重合),且 ,则 能否为等腰三角形?若能,求出 的长;若不能,请说明理由;(3)、若点 在抛物线上,且 ,试确定满足条件的点 的个数.