2017年高考文数真题试卷(山东卷)
试卷更新日期:2017-06-09 类型:高考真卷
一、选择题:本题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 设集合M={x||x﹣1|<1},N={x|x<2},则M∩N=( )A、(﹣1,1) B、(﹣1,2) C、(0,2) D、(1,2)2. 已知i是虚数单位,若复数z满足zi=1+i,则z2=( )A、﹣2i B、2i C、﹣2 D、23. 已知x,y满足约束条件 则z=x+2y的最大值是( )A、﹣3 B、﹣1 C、1 D、34. 已知cosx= ,则cos2x=( )A、﹣ B、 C、﹣ D、5. 已知命题p:∃x∈R,x2﹣x+1≥0.命题q:若a2<b2 , 则a<b,下列命题为真命题的是( )A、p∧q B、p∧¬q C、¬p∧q D、¬p∧¬q6.
若执行右侧的程序框图,当输入的x的值为4时,输出的y的值为2,则空白判断框中的条件可能为( )
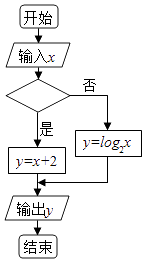 A、x>3 B、x>4 C、x≤4 D、x≤57. 函数y= sin2x+cos2x的最小正周期为( )A、 B、 C、π D、2π8.
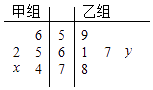
A、x>3 B、x>4 C、x≤4 D、x≤57. 函数y= sin2x+cos2x的最小正周期为( )A、 B、 C、π D、2π8.如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
 A、3,5 B、5,5 C、3,7 D、5,79. 设f(x)= 若f(a)=f(a+1),则f( )=( )A、2 B、4 C、6 D、810. 若函数exf(x)(e=2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称f(x)具有M性质,下列函数中具有M性质的是( )A、f(x)=2x B、f(x)=x2 C、f(x)=3﹣x D、f(x)=cosx
A、3,5 B、5,5 C、3,7 D、5,79. 设f(x)= 若f(a)=f(a+1),则f( )=( )A、2 B、4 C、6 D、810. 若函数exf(x)(e=2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称f(x)具有M性质,下列函数中具有M性质的是( )A、f(x)=2x B、f(x)=x2 C、f(x)=3﹣x D、f(x)=cosx二、填空题:本大题共5小题,每小题5分,共25分
-
11. 已知向量 =(2,6), =(﹣1,λ),若 ,则λ= .12. 若直线 =1(a>0,b>0)过点(1,2),则2a+b的最小值为 .13.
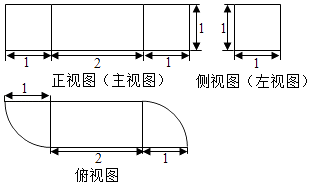
由一个长方体和两个 圆柱体构成的几何体的三视图如图,则该几何体的体积为 .
 14. 已知f(x)是定义在R上的偶函数,且f(x+4)=f(x﹣2).若当x∈[﹣3,0]时,f(x)=6﹣x , 则f(919)= .15. 在平面直角坐标系xOy中,双曲线 =1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
14. 已知f(x)是定义在R上的偶函数,且f(x+4)=f(x﹣2).若当x∈[﹣3,0]时,f(x)=6﹣x , 则f(919)= .15. 在平面直角坐标系xOy中,双曲线 =1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .三、解答题
-
16. 某旅游爱好者计划从3个亚洲国家A1 , A2 , A3和3个欧洲国家B1 , B2 , B3中选择2个国家去旅游.
(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
17. 在△ABC中,角A,B,C的对边分别为a,b,c,已知b=3, =﹣6,S△ABC=3,求A和a.18. 由四棱柱ABCD﹣A1B1C1D1截去三棱锥C1﹣B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,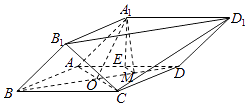
(Ⅰ)证明:A1O∥平面B1CD1;
(Ⅱ)设M是OD的中点,证明:平面A1EM⊥平面B1CD1 .
19. 已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3 .(1)、求数列{an}通项公式;(2)、{bn} 为各项非零的等差数列,其前n项和为Sn , 已知S2n+1=bnbn+1 , 求数列 的前n项和Tn .20. 已知函数f(x)= x3﹣ ax2 , a∈R,(1)、当a=2时,求曲线y=f(x)在点(3,f(3))处的切线方程;(2)、设函数g(x)=f(x)+(x﹣a)cosx﹣sinx,讨论g(x)的单调性并判断有无极值,有极值时求出极值.21.在平面直角坐标系xOy中,已知椭圆C: =1(a>b>0)的离心率为 ,椭圆C截直线y=1所得线段的长度为2 .
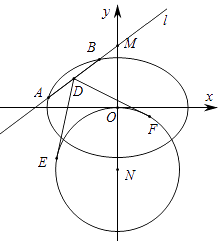
(Ⅰ)求椭圆C的方程;
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|.设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求∠EDF的最小值.