2017年高考文数真题试卷（北京卷）

试卷更新日期：2017-06-09 类型：高考真卷

进入出卷网下载

一、选择题

1. 已知全集U=R，集合A={x|x＜﹣2或x＞2}，则∁_UA=（　　）

A、（﹣2，2） B、（﹣∞，﹣2）∪（2，+∞） C、[﹣2，2] D、（﹣∞，﹣2]∪[2，+∞）

查看试题解析
2. 若复数（1﹣i）（a+i）在复平面内对应的点在第二象限，则实数a的取值范围是（　　）

A、（﹣∞，1） B、（﹣∞，﹣1） C、（1，+∞） D、（﹣1，+∞）

查看试题解析
3.
执行如图所示的程序框图，输出的S值为（　　）

A、2 B、 $\frac{3}{2}$ C、 $\frac{5}{3}$ D、 $\frac{8}{5}$

查看试题解析
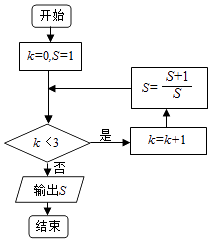4. 若x，y满足 ${\begin{matrix} x \leq 3 \\ x + y \geq 2 \\ y \leq x \end{matrix}$ ，则x+2y的最大值为（　　）

A、1 B、3 C、5 D、9

查看试题解析
5. 已知函数f（x）=3^x﹣（ $\frac{1}{3}$ ）^x ，则f（x）（　　）

A、是偶函数，且在R上是增函数 B、是奇函数，且在R上是增函数 C、是偶函数，且在R上是减函数 D、是奇函数，且在R上是减函数

查看试题解析
6.
某三棱锥的三视图如图所示，则该三棱锥的体积为（　　）

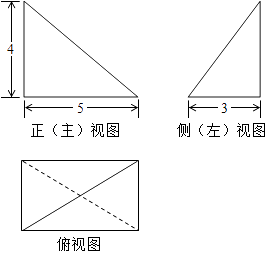A、60 B、30 C、20 D、10

查看试题解析
7. 设 $\vec{m}$ ， $\vec{n}$ 为非零向量，则“存在负数λ，使得 $\vec{m}$ =λ $\vec{n}$ ”是 $\vec{m}$ • $\vec{n}$ ＜0”的（　　）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
8. 根据有关资料，围棋状态空间复杂度的上限M约为3³⁶¹ ，而可观测宇宙中普通物质的原子总数N约为10⁸⁰ ，则下列各数中与 $\frac{M}{N}$ 最接近的是（　　）
（参考数据：lg3≈0.48）

A、10³³ B、10⁵³ C、10⁷³ D、10⁹³

查看试题解析

二、填空题

9. 在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称，若sinα= $\frac{1}{3}$ ，则sinβ= ．

查看试题解析
10. 若双曲线x²﹣ $\frac{y^{2}}{m}$ =1的离心率为 $\sqrt{3}$ ，则实数m= ．

查看试题解析
11. 已知x≥0，y≥0，且x+y=1，则x²+y²的取值范围是．

查看试题解析
12. 已知点P在圆x²+y²=1上，点A的坐标为（﹣2，0），O为原点，则 $\vec{A O}$ • $\vec{A P}$ 的最大值为．

查看试题解析
13. 能够说明“设a，b，c是任意实数．若a＞b＞c，则a+b＞c”是假命题的一组整数a，b，c的值依次为．

查看试题解析
14. 某学习小组由学生和教师组成，人员构成同时满足以下三个条件：
（i）男学生人数多于女学生人数；
（ii）女学生人数多于教师人数；
（iii）教师人数的两倍多于男学生人数．
①若教师人数为4，则女学生人数的最大值为．
②该小组人数的最小值为．

查看试题解析

三、解答题

15. 已知等差数列{a_n}和等比数列{b_n}满足a₁=b₁=1，a₂+a₄=10，b₂b₄=a₅ ．
（Ⅰ）求{a_n}的通项公式；
（Ⅱ）求和：b₁+b₃+b₅+…+b_2n_﹣₁ ．

查看试题解析
16. 已知函数f（x）= $\sqrt{3}$ cos（2x﹣ $\frac{π}{3}$ ）﹣2sinxcosx．（13分）

（Ⅰ）求f（x）的最小正周期；
（Ⅱ）求证：当x∈[﹣ $\frac{π}{4}$ ， $\frac{π}{4}$ ]时，f（x）≥﹣ $\frac{1}{2}$ ．

查看试题解析
17.
某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20，30），[30，40），…[80，90]，并整理得到如下频率分布直方图：

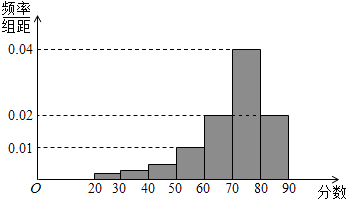
（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；
（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40，50）内的人数；
（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．

查看试题解析
18.
如图，在三棱锥P﹣ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．

(1)、求证：PA⊥BD；

(2)、求证：平面BDE⊥平面PAC；

(3)、当PA∥平面BDE时，求三棱锥E﹣BCD的体积．

查看试题解析
19. 已知椭圆C的两个顶点分别为A（﹣2，0），B（2，0），焦点在x轴上，离心率为 $\frac{\sqrt{3}}{2}$ ．

（Ⅰ）求椭圆C的方程；
（Ⅱ）点D为x轴上一点，过D作x轴的垂线交椭圆C于不同的两点M，N，过D作AM的垂线交BN于点E．求证：△BDE与△BDN的面积之比为4：5．

查看试题解析
20. 已知函数f（x）=e^xcosx﹣x．

(1)、求曲线y=f（x）在点（0，f（0））处的切线方程；

(2)、求函数f（x）在区间[0， $\frac{π}{2}$ ]上的最大值和最小值．

查看试题解析