2017年高考文数真题试卷（新课标Ⅱ卷）

试卷更新日期：2017-06-09 类型：高考真卷

进入出卷网下载

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 设集合A={1，2，3}，B={2，3，4}，则A∪B=（）

A、{1，2，3，4} B、{1，2，3} C、{2，3，4} D、{1，3，4}

查看试题解析
2. （1+i）（2+i）=（）

A、1﹣i B、1+3i C、3+i D、3+3i

查看试题解析
3. 函数f（x）=sin（2x+ $\frac{π}{3}$ ）的最小正周期为（）

A、4π B、2π C、π D、 $\frac{π}{2}$

查看试题解析
4. 设非零向量 $\vec{a}$ ， $\vec{b}$ 满足| $\vec{a}$ + $\vec{b}$ |=| $\vec{a}$ ﹣ $\vec{b}$ |则（）

A、 $\vec{a}$ ⊥ $\vec{b}$ B、| $\vec{a}$ |=| $\vec{b}$ | C、 $\vec{a}$ ∥ $\vec{b}$ D、| $\vec{a}$ |＞| $\vec{b}$ |

查看试题解析
5. 若a＞1，则双曲线 $\frac{x^{2}}{a^{2}}$ ﹣y²=1的离心率的取值范围是（）

A、（ $\sqrt{2}$ ，+∞） B、（ $\sqrt{2}$ ，2） C、（1， $\sqrt{2}$ ） D、（1，2）

查看试题解析
6.
如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）

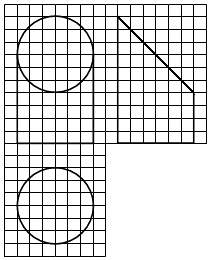A、90π B、63π C、42π D、36π

查看试题解析
7. 设x，y满足约束条件 ${\begin{matrix} 2 x + 3 y - 3 \leq 0 \\ 2 x - 3 y + 3 \geq 0 \\ y + 3 \geq 0 \end{matrix}$ ，则z=2x+y的最小值是（）

A、﹣15 B、﹣9 C、1 D、9

查看试题解析
8. 函数f（x）=ln（x²﹣2x﹣8）的单调递增区间是（）

A、（﹣∞，﹣2） B、（﹣∞，﹣1） C、（1，+∞） D、（4，+∞）

查看试题解析
9. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩，老师说，你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩，看后甲对大家说：我还是不知道我的成绩，根据以上信息，则（）

A、乙可以知道两人的成绩 B、丁可能知道两人的成绩 C、乙、丁可以知道对方的成绩 D、乙、丁可以知道自己的成绩

查看试题解析
10.
执行如图的程序框图，如果输入的a=﹣1，则输出的S=（）

A、2 B、3 C、4 D、5

查看试题解析
11. 从分别写有1，2，3，4，5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为（）

A、 $\frac{1}{10}$ B、 $\frac{1}{5}$ C、 $\frac{3}{10}$ D、 $\frac{2}{5}$

查看试题解析
12. 过抛物线C：y²=4x的焦点F，且斜率为 $\sqrt{3}$ 的直线交C于点M（M在x轴上方），l为C的准线，点N在l上，且MN⊥l，则M到直线NF的距离为（）

A、 $\sqrt{5}$ B、2 $\sqrt{2}$ C、2 $\sqrt{3}$ D、3 $\sqrt{3}$

查看试题解析

二、填空题，本题共4小题，每小题5分，共20分

13. 函数f（x）=2cosx+sinx的最大值为．

查看试题解析
14. 已知函数f（x）是定义在R上的奇函数，当x∈（﹣∞，0）时，f（x）=2x³+x² ，则f（2）= ．

查看试题解析
15. 长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为．

查看试题解析
16. △ABC的内角A，B，C的对边分别为a，b，c，若2bcosB=acosC+ccosA，则B= ．

查看试题解析

三、解答题

17. 已知等差数列{a_n}的前n项和为S_n ，等比数列{b_n}的前n项和为T_n ， a₁=﹣1，b₁=1，a₂+b₂=2．
（Ⅰ）若a₃+b₃=5，求{b_n}的通项公式；
（Ⅱ）若T₃=21，求S₃ ．

查看试题解析
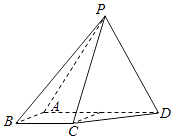
18. 如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC= $\frac{1}{2}$ AD，∠BAD=∠ABC=90°．
（Ⅰ）证明：直线BC∥平面PAD；

（Ⅱ）若△PCD面积为2 $\sqrt{7}$ ，求四棱锥P﹣ABCD的体积．

查看试题解析
19. 海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg），其频率分布直方图如下：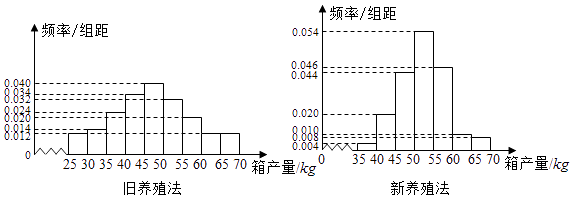
（Ⅰ）记A表示时间“旧养殖法的箱产量低于50kg”，估计A的概率；
（Ⅱ）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：

箱产量＜50kg
箱产量≥50kg
旧养殖法

新养殖法

（Ⅲ）根据箱产量的频率分布直方图，对两种养殖方法的优劣进行比较．
附：
P（K²≥K）
0.050
0.010
0.001
K
3.841
6.635
10.828
K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ．

查看试题解析
20. 设O为坐标原点，动点M在椭圆C： $\frac{x^{2}}{2}$ +y²=1上，过M做x轴的垂线，垂足为N，点P满足 $\vec{N P}$ = $\sqrt{2} \vec{N M}$ ．
（Ⅰ）求点P的轨迹方程；
（Ⅱ）设点Q在直线x=﹣3上，且 $\vec{O P}$ • $\vec{P Q}$ =1．证明：过点P且垂直于OQ的直线l过C的左焦点F．

查看试题解析
21. 设函数f（x）=（1﹣x²）e^x ．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）当x≥0时，f（x）≤ax+1，求a的取值范围．

查看试题解析
22. 在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C₁的极坐标方程为ρcosθ=4．

（Ⅰ）M为曲线C₁上的动点，点P在线段OM上，且满足|OM|•|OP|=16，求点P的轨迹C₂的直角坐标方程；

（Ⅱ）设点A的极坐标为（2， $\frac{π}{3}$ ），点B在曲线C₂上，求△OAB面积的最大值．

查看试题解析
23. 已知a＞0，b＞0，a³+b³=2，证明：

（Ⅰ）（a+b）（a⁵+b⁵）≥4；

（Ⅱ）a+b≤2．

查看试题解析

	箱产量＜50kg	箱产量≥50kg
旧养殖法
新养殖法

P（K²≥K）	0.050	0.010	0.001
K	3.841	6.635	10.828