2017年高考理数真题试卷（新课标Ⅱ卷）

试卷更新日期：2017-06-09 类型：高考真卷

进入出卷网下载

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. $\frac{3 + i}{1 + i}$ =（）

A、1+2i B、1﹣2i C、2+i D、2﹣i

查看试题解析
2. 设集合A={1，2，4}，B={x|x²﹣4x+m=0}．若A∩B={1}，则B=（）

A、{1，﹣3} B、{1，0} C、{1，3} D、{1，5}

查看试题解析
3. 我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（）

A、1盏 B、3盏 C、5盏 D、9盏

查看试题解析
4.
如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）

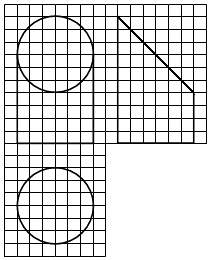A、90π B、63π C、42π D、36π

查看试题解析
5. 设x，y满足约束条件 ${\begin{matrix} 2 x + 3 y - 3 \leq 0 \\ 2 x - 3 y + 3 \geq 0 \\ y + 3 \geq 0 \end{matrix}$ ，则z=2x+y的最小值是（）

A、﹣15 B、﹣9 C、1 D、9

查看试题解析
6. 安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有（）

A、12种 B、18种 C、24种 D、36种

查看试题解析
7. 甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则（）

A、乙可以知道四人的成绩 B、丁可以知道四人的成绩 C、乙、丁可以知道对方的成绩 D、乙、丁可以知道自己的成绩

查看试题解析
8.
执行如图的程序框图，如果输入的a=﹣1，则输出的S=（）

A、2 B、3 C、4 D、5

查看试题解析
9. 若双曲线C： $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的一条渐近线被圆（x﹣2）²+y²=4所截得的弦长为2，则C的离心率为（）

A、2 B、 $\sqrt{3}$ C、 $\sqrt{2}$ D、 $\frac{2 \sqrt{3}}{3}$

查看试题解析
10. 已知直三棱柱ABC﹣A₁B₁C₁中，∠ABC=120°，AB=2，BC=CC₁=1，则异面直线AB₁与BC₁所成角的余弦值为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{15}}{5}$ C、 $\frac{\sqrt{10}}{5}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
11. 若x=﹣2是函数f（x）=（x²+ax﹣1）e^x^﹣1的极值点，则f（x）的极小值为（）

A、﹣1 B、﹣2e^﹣3 C、5e^﹣3 D、1

查看试题解析
12. 已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则 $\vec{P A}$ •（ $\vec{P B}$ + $\vec{P C}$ ）的最小值是（）

A、﹣2 B、﹣ $\frac{3}{2}$ C、﹣ $\frac{4}{3}$ D、﹣1

查看试题解析

二、填空题：本题共4小题，每小题5分，共20分.

13. 一批产品的二等品率为0.02，从这批产品中每次随机取一件，有放回地抽取100次，X表示抽到的二等品件数，则DX= ．

查看试题解析
14. 函数f（x）=sin²x+ $\sqrt{3}$ cosx﹣ $\frac{3}{4}$ （x∈[0， $\frac{π}{2}$ ]）的最大值是．

查看试题解析
15. 等差数列{a_n}的前n项和为S_n ， a₃=3，S₄=10，则 $\sum_{k = 1}^{n} \frac{1}{S_{k}}$ = ．

查看试题解析
16. 已知F是抛物线C：y²=8x的焦点，M是C上一点，FM的延长线交y轴于点N．若M为FN的中点，则|FN|= ．

查看试题解析

三、解答题

17. △ABC的内角A，B，C的对边分别为a，b，c，已知sin（A+C）=8sin² $\frac{B}{2}$ ．
（Ⅰ）求cosB；
（Ⅱ）若a+c=6，△ABC面积为2，求b．

查看试题解析
18.
海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100 个网箱，测量各箱水产品的产量（单位：kg），其频率分布直方图如图：
（Ⅰ）设两种养殖方法的箱产量相互独立，记A表示事件“旧养殖法的箱产量低于50kg，新养殖法的箱产量不低于50kg”，估计A的概率；
（Ⅱ）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：

箱产量＜50kg
         箱产量≥50kg
旧养殖法


新养殖法


（Ⅲ）根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到0.01）．
附：
P（K²≥k）
0.050
0.010
0.001
K
3.841
6.635
10.828
K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ．

查看试题解析
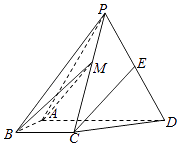
19.
如图，四棱锥P﹣ABCD中，侧面PAD为等边三角形且垂直于底面ABCD，AB=BC= $\frac{1}{2}$ AD，∠BAD=∠ABC=90°，E是PD的中点．
（Ⅰ）证明：直线CE∥平面PAB；
（Ⅱ）点M在棱PC 上，且直线BM与底面ABCD所成角为45°，求二面角M﹣AB﹣D的余弦值．

查看试题解析
20. 设O为坐标原点，动点M在椭圆C： $\frac{x^{2}}{2}$ +y²=1上，过M做x轴的垂线，垂足为N，点P满足 $\vec{N P}$ = $\sqrt{2} \vec{N M}$ ．
（Ⅰ）求点P的轨迹方程；
（Ⅱ）设点Q在直线x=﹣3上，且 $\vec{O P}$ • $\vec{P Q}$ =1．证明：过点P且垂直于OQ的直线l过C的左焦点F．

查看试题解析
21. 已知函数f（x）=ax²﹣ax﹣xlnx，且f（x）≥0．
（Ⅰ）求a；
（Ⅱ）证明：f（x）存在唯一的极大值点x₀ ，且e^﹣2＜f（x₀）＜2^﹣2 ．

查看试题解析
22. 在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C₁的极坐标方程为ρcosθ=4．

（Ⅰ）M为曲线C₁上的动点，点P在线段OM上，且满足|OM|•|OP|=16，求点P的轨迹C₂的直角坐标方程；

（Ⅱ）设点A的极坐标为（2， $\frac{π}{3}$ ），点B在曲线C₂上，求△OAB面积的最大值．

查看试题解析
23. 已知a＞0，b＞0，a³+b³=2，证明：

（Ⅰ）（a+b）（a⁵+b⁵）≥4；

（Ⅱ）a+b≤2．

查看试题解析

	箱产量＜50kg	箱产量≥50kg
旧养殖法
新养殖法

P（K²≥k）	0.050	0.010	0.001
K	3.841	6.635	10.828