安徽省滁州市2018-2019学年高一下学期数学6月月考联考试卷

试卷更新日期：2019-07-17 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12小题，共60分）

1. 设集合A={x|x²-4x+3<0}，B={x|2x-3>0}，则A∩B=（）

A、（-3， $- \frac{3}{2}$ ） B、（-3， $\frac{3}{2}$ ） C、（1， $\frac{3}{2}$ ） D、（ $\frac{3}{2}$ ，3）

查看试题解析
2. 设a，b，c∈B，且a>b，则（）

A、ac>bc B、a-c<b-c C、a²>b² D、a³>b³

查看试题解析
3. 设△ABC的内角A，B，C所对边分别为a．b．c若a=3，b= $\sqrt{3}$ ，A= $\frac{π}{3}$ ，则B=（）

A、 $\frac{π}{6}$ B、 $\frac{5 π}{6}$ C、 $\frac{π}{6}$ 或 $\frac{5 π}{6}$ D、 $\frac{2 π}{3}$

查看试题解析
4. 已知等差数列{a_n}前9项的和为27，a₁₀=8，则a₁₀₀=（）

A、100 B、99 C、98 D、97

查看试题解析
5. 已知m，n是两条不同的直线，a，β是两个不同的平面，则下列命题正确的是（）

A、若m∥n，m⊥a，则n⊥a． B、若m∥a，n∥a，则m∥n C、若m⊥a，m∥B，则a∥β． D、若m∥a，a⊥β，则m⊥β

查看试题解析
6. 已知等比数列{an}中，a₁+a₂=3，a₃+a₄=12，则a₅+a₆=( ）．

A、3 B、15 C、48 D、63

查看试题解析
7. 当x∈R时，不等式kx²-kx+1>0恒成立，则k的取值范围是（）

A、（0，+∞) B、[0，+∞) C、[0，4) D、（0，4）

查看试题解析
8. 已知等差数列{an}的前n项为S_n ，且a₁+a₅=-14，S₉=-27，则使得S_n取最小值时的n为（）

A、1 B、6 C、7 D、6或7

查看试题解析
9. 在正方体ABCD-A₁B₁C₁D₁中，E为棱CD的中点，则（）

A、A₁E⊥DC₁ B、A₁E⊥BD C、A₁E⊥BC₁ D、A₁E⊥AC

查看试题解析
10. 在△ABC中，角A、B、C所对的边分别为a、b、c，且b²+c²=a²+bc.若sinB·sinC=sin²A,则△ABC的形状是（）

A、等腰三角形 B、直角三角形 C、等边三角形 D、等腰直角三角形

查看试题解析
11. 某几何体的三视图如图所示，则该几何体的体积为（）

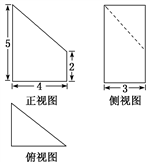A、12 B、18 C、24 D、30

查看试题解析
12. △ABC中，a．b．c分别为∠A．∠B．∠C的对边，如果a．b．c成等差数列，∠B=30°，△ABC的面积为 $\frac{3}{2}$ ，那么b等于（）

A、 $\frac{1 + \sqrt{3}}{2}$ B、1+ $\sqrt{3}$ C、 $\frac{2 + \sqrt{3}}{2}$ D、2+ $\sqrt{3}$

查看试题解析

二、填空题（本大题共4小题，共20分）

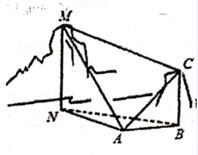
13. 若x，y满足约束条件 ${\begin{cases} x - y + 1 \geq 0 \\ x + y - 3 \geq 0 \\ x - 3 \leq 0 \end{cases}$ ，则z=x-2y的最小值为．

查看试题解析
14. 已知正实数x，y满足2x+y=1，则xy的最大值为．

查看试题解析
15. 设等比数列{a_n}满足a₁+a₃=10，a₂+a₄=5，则a₁a₂…a_n的最大值为．

查看试题解析
16. 如图，为测量山高MN，选择A和另一座的山顶C为测量观测点，从A点测得M点的仰角∠NAM=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°，已知山高BC=1000m，则山高MN=m．

查看试题解析

三、解答题（本大题共6小题，17题10分，其它均为12分，共70分）

17. 如图，某货轮在A处看灯塔层在货轮的北偏东75°，距离为6海里，在A处看灯塔C在货轮的北偏西30°，距离为4海里，货轮由A处向正北航行到D处时，再看灯塔B在北偏东120°，求：

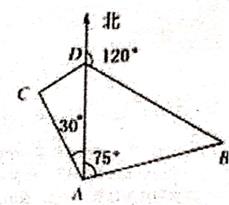(1)、A处与D处的距离；

(2)、灯塔C与D处的距离。

查看试题解析
18. 已知公差不为零的等差数列{an}满足：a₃+a₈=20，且a₅是a₂与a₁₄的等比中项。

(1)、求数列{an}的通项公式；

(2)、设数列{bn}时满足bn= $\frac{1}{a_{n} a_{n + 1}}$ ；求数列{bn}的前n项和S_n ．

查看试题解析
19. 在△ABC中，角A、B、C所对的边分别为a、b、c，且a=2，cosB= $\frac{3}{5}$

(1)、若b=4，求sinA的值；

(2)、若△ABC的面积 S_△ABC=4，求b、c的值．

查看试题解析
20. 如图，某学校准备修建一个面积为2400平方米的矩形活动场地（图中ABCD）的围栏，按照修建要求，中间用围墙EF隔开，使得ABEF为矩形，EFCD为正方形，设AB=x米，已知围墙（包括EF）的修建费用均为每米500元，设围墙（包括EF）的修建总费用为y元。

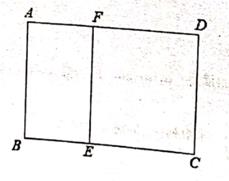(1)、求出y关于x的函数解析式及x的取值范围。

(2)、当x为何值时，围墙（包括EF）的修建总费用y最小？并求出y的最小值。

查看试题解析
21. 在四棱锥E-ABCD中，底面ABCD是正方形，AC与BD交于点O，EC⊥底面ABCD，F为BE的中点。

(Ⅰ)求证：DE∥平面ACF

（Ⅱ）求证：BD⊥AE；

（Ⅲ）若AB= $\sqrt{2}$ CE=2，求三棱锥F-ABC的体积，

查看试题解析
22. 已知数列{a_n}的前n项和为S_n ，且S_n+1=4_an+2 ， a₁=1．

(1)、b_n=a_n+1-2a_n ，求证数列{b_n}是等比数列；

(2)、设c_n= $\frac{a_{n}}{2^{n}}$ ，求证数列{c_n}是等差数列；

(3)、求数列{a_n}的通项公式及前n项和S_n。

查看试题解析