江西省九江市2018-2019学年高二下学期理数期末考试试卷
试卷更新日期:2019-07-17 类型:期末考试
一、单选题
-
1. 已知复数 满足 ,则 ( )A、 B、 C、 D、2. ( )A、 B、 C、 D、3. 某校团委对“学生性别与中学生追星是否有关”作了一次调查,利用 列联表,由计算得 ,参照下表:
0.01
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
得到正确结论是( )
A、有99%以上的把握认为“学生性别与中学生追星无关” B、有99%以上的把握认为“学生性别与中学生追星有关” C、在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星无关” D、在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星有关”4. 展开式中常数项为( )A、 B、 C、 D、5. 函数 有( )A、最大值为1 B、最小值为1 C、最大值为 D、最小值为6. 设随机变量 ,若 ,则 ( )A、 B、 C、 D、7. 甲乙丙丁四人参加数学竞赛,其中只有一位获奖.有人走访了四人,甲说:“乙、丁都未获奖.”乙说:“是甲或丙获奖.”丙说:“是甲获奖.”丁说:“是乙获奖.”四人所说话中只有两位是真话,则获奖的人是( )A、甲 B、乙 C、丙 D、丁8. 已知 ,则 的值( )A、都大于1 B、都小于1 C、至多有一个不小于1 D、至少有一个不小于19. 学校新入职的5名教师要参加由市教育局组织的暑期3期上岗培训,每人只参加其中1期培训,每期至多派2人,由于时间上的冲突,甲教师不能参加第一期培训,则学校不同的选派方法有( )A、 种 B、 种 C、 种 D、 种10. 2019年,河北等8省公布了高考改革综合方案将采取“3+1+2”模式,即语文、数学、英语必考,然后考生先在物理、历史中选择1门,再在思想政治、地理、化学、生物中选择2门.一名同学随机选择3门功课,则该同学选到物理、地理两门功课的概率为( )A、 B、 C、 D、11. 设 , , ,则 大小关系是( )A、 B、 C、 D、12. 设 , , ,则 大小关系是( )A、 B、 C、 D、13. 已知函数 的导函数为 ,满足 , 且 ,则不等式 的解集为( )A、 B、 C、 D、14. 已知函数 ( )在 上的最大值为3,则 ( )A、 B、 C、 D、二、填空题
-
15. 若复数 ( )为纯虚数,则 .16. 已知某公司生产的一种产品的质量 (单位:千克)服从正态分布 .现从该产品的生产线上随机抽取 件产品,则其中质量在区间 内的产品估计有件.
附:若 ,则 , .
17. 如图,矩形 中曲线的方程分别为 , ,在矩形内随机取一点,则此点取自阴影部分的概率为.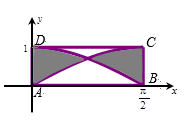 18. 在 中,角 所对的边分别为 ,已知 ,则 .19. 在 中,角 所对的边分别为 ,已知 ,且 的面积为 ,则 的周长为.
18. 在 中,角 所对的边分别为 ,已知 ,则 .19. 在 中,角 所对的边分别为 ,已知 ,且 的面积为 ,则 的周长为.三、解答题
-
20. 在某项体能测试中,规定每名运动员必需参加且最多两次,一旦第一次测试通过则不再参加第二次测试,否则将参加第二次测试.已知甲每次通过的概率为 ,乙每次通过的概率为 ,且甲乙每次是否通过相互独立.
(Ⅰ)求甲乙至少有一人通过体能测试的概率;
(Ⅱ)记 为甲乙两人参加体能测试的次数和,求 的分布列和期望.
21. 中,三内角 所对的边分别为 ,已知 成等差数列.(Ⅰ)求证: ;
(Ⅱ)求角 的取值范围.
22. 已知数列 满足 , .(Ⅰ)求 的值,猜想数列 的通项公式并用数学归纳法证明;
(Ⅱ)令 ,求数列 的前 项和 .
23. 使用支付宝和微信支付已经成为广大消费者最主要的消费支付方式,某超市通过统计发现一周内超市每天的净利润 (万元)与每天使用支付宝和微信支付的人数 (千人)具有相关关系,并得到最近一周 的7组数据如下表,并依此作为决策依据.周一
周二
周三
周四
周五
周六
周日
13
16
26
22
25
29
30
7
11
15
22
24
27
34
(Ⅰ)作出散点图,判断 与 哪一个适合作为每天净利润的回归方程类型?并求出回归方程( , , , 精确到 );

(Ⅱ)超市为了刺激周一消费,拟在周一开展使用支付宝和微信支付随机抽奖活动,总奖金7万元.根据市场调查,抽奖活动能使使用支付宝和微信支付消费人数增加6千人,7千人,8千人,9千人的概率依次为 , , , .试决策超市是否有必要开展抽奖活动?
参考数据: , , , .
参考公式: , , .
24. 已知函数 ( ).(Ⅰ)当 时,求曲线 在 处的切线方程;
(Ⅱ)若对任意 , 恒成立,求实数 的取值范围.
25. 已知函数 ( ).(Ⅰ)若 在 处的切线过点 ,求 的值;
(Ⅱ)若 恰有两个极值点 , ( ).
(ⅰ)求 的取值范围;
(ⅱ)求证: .
26. 在平面直角坐标系 中,直线 的普通方程为 ,曲线 的参数方程为 ( 为参数),以 为极点, 轴的正半轴为极轴建立极坐标系.(Ⅰ)求直线 的参数方程和极坐标方程;
(Ⅱ)设直线 与曲线 相交于 两点,求 的值.