江苏省盐城市2018-2019学年高二下学期数学期末考试试卷
试卷更新日期:2019-07-17 类型:期末考试
一、填空题
-
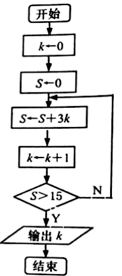
1. 已知复数 , (其中 为虚数单位),若 为实数,则实数 的值为 .2. 已知一组数据 , , , , 的方差为 ,则数据2 ,2 ,2 ,2 ,2 的方差为 .3. 某学校拟从2名男教师和1名女教师中随机选派2名教师去参加一个教师培训活动,则2名男教师去参加培训的概率是 .4. 若命题“ ,使得 成立”是假命题,则实数 的取值范围是 .5. 执行如图所示的流程图,则输出 的值为 .
 6. 已知实数 满足 ,则 的最大值为 .7. 若双曲线 的两条渐近线与抛物线 的准线围成的三角形面积为 ,则双曲线 的离心率为 .8. 已知圆: 的面积为 ,类似的,椭圆: 的面积为 .
6. 已知实数 满足 ,则 的最大值为 .7. 若双曲线 的两条渐近线与抛物线 的准线围成的三角形面积为 ,则双曲线 的离心率为 .8. 已知圆: 的面积为 ,类似的,椭圆: 的面积为 .
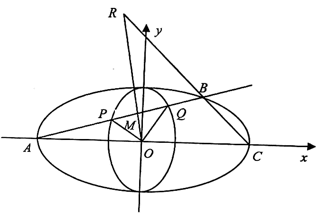
9. 5名学生站成一排拍照片,其中甲乙两名学生不相邻的站法有种.(结果用数值表示)10. 已知函数 的一条对称轴为 ,则 的值为 .11. 在 的二项展开式中,常数项为(结果用数值表示)12. 若函数 且 是偶函数,则函数 的值域为 .13. 已知函数 ,则“ ”是“函数 有且仅有一个极值点”的条件.(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)14. 设 分别为椭圆 的右顶点和上顶点,已知椭圆 过点 ,当线段 长最小时椭圆 的离心率为 .15. 若 为正实数,则 的最大值为 .16. 已知函数 , 的最大值为 ,则实数 的值为 .二、解答题
-
17. 如图,在四棱锥 中,已知底面 为菱形, , , 为对角线 与 的交点, 底面 且
 (1)、求异面直线 与 所成角的余弦值;(2)、求平面 与平面 所成锐二面角的余弦值.18. 设命题 函数 在 是减函数;命题 ,都有 成立.(1)、若命题 为真命题,求实数 的取值范围;(2)、若 为真命题, 为假命题,求实数 的取值范围.19. 某超市在节日期间进行有奖促销,凡在该超市购物满 元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有 只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励 元;共两只球都是绿色,则奖励 元;若两只球颜色不同,则不奖励.(1)、求一名顾客在一次摸奖活动中获得 元的概率;(2)、记 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量 的分布列和数学期望.20. 设函数 .(1)、若函数 为奇函数, (0, ),求 的值;(2)、若 = , = , (0, ),求 的值.21. 已知数列 各项均为正数,满足 .(1)、求 , , 的值;(2)、猜想数列 的通项公式,并用数学归纳法证明你的结论.22. 设 , .(1)、证明:对任意实数 ,函数 都不是奇函数;(2)、当 时,求函数 的单调递增区间.23. 如图,一条小河岸边有相距 的 两个村庄(村庄视为岸边上 两点),在小河另一侧有一集镇 (集镇视为点 ), 到岸边的距离 为 ,河宽 为 ,通过测量可知, 与 的正切值之比为 .当地政府为方便村民出行,拟在小河上建一座桥 ( 分别为两岸上的点,且 垂直河岸, 在 的左侧),建桥要求:两村所有人到集镇所走距离之和最短,已知 两村的人口数分别是 人、 人,假设一年中每人去集镇的次数均为 次.设 .(小河河岸视为两条平行直线)
(1)、求异面直线 与 所成角的余弦值;(2)、求平面 与平面 所成锐二面角的余弦值.18. 设命题 函数 在 是减函数;命题 ,都有 成立.(1)、若命题 为真命题,求实数 的取值范围;(2)、若 为真命题, 为假命题,求实数 的取值范围.19. 某超市在节日期间进行有奖促销,凡在该超市购物满 元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有 只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励 元;共两只球都是绿色,则奖励 元;若两只球颜色不同,则不奖励.(1)、求一名顾客在一次摸奖活动中获得 元的概率;(2)、记 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量 的分布列和数学期望.20. 设函数 .(1)、若函数 为奇函数, (0, ),求 的值;(2)、若 = , = , (0, ),求 的值.21. 已知数列 各项均为正数,满足 .(1)、求 , , 的值;(2)、猜想数列 的通项公式,并用数学归纳法证明你的结论.22. 设 , .(1)、证明:对任意实数 ,函数 都不是奇函数;(2)、当 时,求函数 的单调递增区间.23. 如图,一条小河岸边有相距 的 两个村庄(村庄视为岸边上 两点),在小河另一侧有一集镇 (集镇视为点 ), 到岸边的距离 为 ,河宽 为 ,通过测量可知, 与 的正切值之比为 .当地政府为方便村民出行,拟在小河上建一座桥 ( 分别为两岸上的点,且 垂直河岸, 在 的左侧),建桥要求:两村所有人到集镇所走距离之和最短,已知 两村的人口数分别是 人、 人,假设一年中每人去集镇的次数均为 次.设 .(小河河岸视为两条平行直线)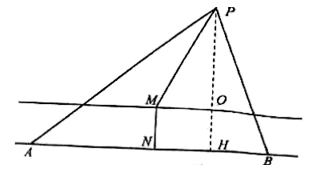 (1)、记 为一年中两村所有人到集镇所走距离之和,试用 表示 ;(2)、试确定 的余弦值,使得 最小,从而符合建桥要求.
(1)、记 为一年中两村所有人到集镇所走距离之和,试用 表示 ;(2)、试确定 的余弦值,使得 最小,从而符合建桥要求.