江苏省淮安市2018-2019学年度高一下学期数学期末考试试卷

试卷更新日期：2019-07-15 类型：期末考试

进入出卷网下载

一、单选题

1. l： $2 x - y = 0$ 的斜率为（）

A、﹣2 B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. △ABC中，若A＋C＝3B，则cosB的值为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{1}{2}$ C、 $- \frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
3. l： $2 x + 3 y - 6 = 0$ 与两坐标轴所围成的三角形的面积为（）

A、6 B、1 C、 $\frac{5}{2}$ D、3

查看试题解析
4. 区间[0，5]上任意取一个实数x，则满足x $\in$ [0，1]的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{4}{5}$ C、 $\frac{5}{6}$ D、 $\frac{1}{4}$

查看试题解析
5. 组数据 $x_{1}$ ， $x_{2}$ ，…， $x_{n}$ 的平均值为3，则 $2 x_{1}$ ， $2 x_{2}$ ，…， $2 x_{n}$ 的平均值为（）

A、3 B、6 C、5 D、2

查看试题解析
6. 三条线段的长分别为5，6，8，则用这三条线段（）

A、能组成直角三角形 B、能组成锐角三角形 C、能组成钝角三角形 D、不能组成三角形

查看试题解析
7. 一个正四棱锥的底面边长为2，高为 $\sqrt{3}$ ，则该正四棱锥的全面积为（）

A、8 B、12 C、16 D、20

查看试题解析
8. 直线l： $2 m x + y - m - 1 = 0$ 与圆C： $x^{2} + {(y - 2)}^{2} = 4$ 交于A，B两点，则当弦AB最短时直线l的方程为（）

A、 $2 x - 4 y + 3 = 0$ B、 $x - 4 y + 3 = 0$ C、 $2 x + 4 y + 3 = 0$ D、 $2 x + 4 y + 1 = 0$

查看试题解析
9. 直三棱柱ABC—A₁B₁C₁中，BB₁中点为M，BC中点为N，∠ABC＝120°，AB＝2，BC＝CC₁＝1，则异面直线AB₁与MN所成角的余弦值为（）

A、1 B、 $- \frac{4}{5}$ C、 $- \frac{3}{4}$ D、0

查看试题解析
10. 直角坐标系xOy中，已知点P(2﹣t，2t﹣2)，点Q(﹣2，1)，直线l： $a x + b y = 0$ ．若对任意的t $\in$ R，点P到直线l的距离为定值，则点Q关于直线l对称点Q′的坐标为（）

A、(0，2) B、(2，3) C、( $\frac{2}{5}$ ， $\frac{11}{5}$ ) D、( $\frac{2}{5}$ ，3)

查看试题解析

二、填空题

11. $l_{1} : x + y = 0$ ， $l_{2} : a x + y + 1 = 0$ ，若 $l_{1} / / l_{2}$ ，则实数 $a$ 的值为．

查看试题解析
12. 高一、高二、高三三个年级共有学生1500人，其中高一共有学生600人，现用分层抽样的方法抽取30人作为样本，则应抽取高一学生数为．

查看试题解析
13. 已知 $Δ$ ABC中， $∠$ A $= 60 °$ ， $a = \sqrt{3}$ ，则 $\frac{a + b + c}{\sin A + \sin B + \sin C}$ = ．

查看试题解析
14. 一个长方体的三个面的面积分别是 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{6}$ ，则这个长方体的体积为.

查看试题解析
15. 圆 ${(x - 2 a)}^{2} + {(y - a - 3)}^{2} = 4$ 上总存在两点到坐标原点的距离为1，则实数a的取值范围是.

查看试题解析
16. △ABC中，角A ， B ， C所对的边分别为a ， b ， c ，若acosB＝5bcosA ， asinA﹣bsinB＝2sinC ，则边c的值为．

查看试题解析

三、解答题

17. 已知三点A(5，0)，B(﹣3，﹣2)，C(0，2)．

(1)、求直线AB的方程；

(2)、求BC的中点到直线AB的距离．

查看试题解析
18. 如图，在△ABC中，B＝30°，D是BC边上一点，AD＝ $4 \sqrt{2}$ ，CD＝7，AC＝5．

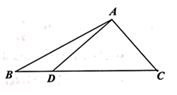(1)、求∠ADC的大小；

(2)、求AB的长．

查看试题解析
19. 甲乙两名篮球运动员分别在各自不同的5场比赛所得篮板球数的茎叶图如图所示，已知两名运动员在各自5场比赛所得平均篮板球数均为10．

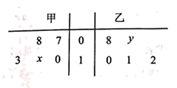(1)、求x，y的值；

(2)、求甲乙所得篮板球数的方差 $S_{甲}^{2}$ 和 $S_{乙}^{2}$ ，并指出哪位运动员篮板球水平更稳定；

(3)、教练员要对甲乙两名运动员篮板球的整体水平进行评估．现在甲乙各自的5场比赛中各选一场进行评估，则两名运动员所得篮板球之和小于18的概率．

查看试题解析
20. 如图，在三棱锥P—ABC中，△PBC为等边三角形，点O为BC的中点，AC⊥PB，平面PBC⊥平面ABC．

(1)、求直线PB和平面ABC所成的角的大小；

(2)、求证：平面PAC⊥平面PBC；

(3)、已知E为PO的中点，F是AB上的点，AF＝ $λ$ AB．若EF∥平面PAC，求 $λ$ 的值．

查看试题解析
21. 如图，圆C与x轴相切于点T(2，0)，与y轴的正半轴相交于A，B两点（A在B的上方），且AB＝3．

(1)、求圆C的方程；

(2)、直线BT上是否存在点P满足PA²＋PB²＋PT²＝12，若存在，求出点P的坐标，若不存在，请说明理由；

(3)、如果圆C上存在E，F两点，使得射线AB平分∠EAF，求证：直线EF的斜率为定值．

查看试题解析