湖北省荆门市2018-2019学年高二下学期数学期末考试试卷
试卷更新日期:2019-07-15 类型:期末考试
一、单选题
-
1. 复数 ( 为虚数单位)的共轭复数是( )A、 B、 C、 D、2. “ ”是“方程 表示焦点在 轴上的双曲线”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 对任意非零实数 ,若 ※ 的运算原理如图所示,则 ※ =( )
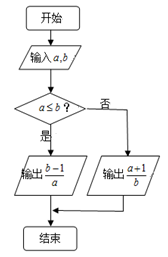 A、1 B、2 C、3 D、44. 下列选项错误的是( )A、“ ”是“ ”的充分不必要条件. B、命题 “若 ,则 ”的逆否命题是“若 ,则 ” C、若命题“ ”,则“ ”. D、若“ ”为真命题,则 均为真命题.5. 观察下列各式: ,则 的末尾两位数字为( )A、49 B、43 C、07 D、016. 已知函数 的导函数为 ,且满足 ,则 ( )A、 B、 C、2 D、-27. 抛物线y2=4x的焦点为F , 点A(3,2),P为抛物线上一点,且P不在直线AF上,则△PAF周长的最小值为( )A、4 B、5 C、 D、8. 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线 为正态分布 的密度曲线)的点的个数的估计值为( )
A、1 B、2 C、3 D、44. 下列选项错误的是( )A、“ ”是“ ”的充分不必要条件. B、命题 “若 ,则 ”的逆否命题是“若 ,则 ” C、若命题“ ”,则“ ”. D、若“ ”为真命题,则 均为真命题.5. 观察下列各式: ,则 的末尾两位数字为( )A、49 B、43 C、07 D、016. 已知函数 的导函数为 ,且满足 ,则 ( )A、 B、 C、2 D、-27. 抛物线y2=4x的焦点为F , 点A(3,2),P为抛物线上一点,且P不在直线AF上,则△PAF周长的最小值为( )A、4 B、5 C、 D、8. 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线 为正态分布 的密度曲线)的点的个数的估计值为( )附:若 ,则 , .
 A、1193 B、1359 C、2718 D、34139. 已知双曲线 , , 是双曲线上关于原点对称的两点, 是双曲线上的动点,直线 , 的斜率分别为 ,若 的最小值为2,则双曲线的离心率为( )A、 B、 C、 D、10. “三个臭皮匠,赛过诸葛亮”,这是我们常说的口头禅,主要是说集体智慧的强大. 假设李某智商较高,他独自一人解决项目M的概率为 ;同时,有 个水平相同的人也在研究项目M , 他们各自独立地解决项目M的概率都是 .现在李某单独研究项目M , 且这 个人组成的团队也同时研究项目M , 设这个 人团队解决项目M的概率为 ,若 ,则 的最小值是( )A、3 B、4 C、5 D、611. 已知椭圆 的左、右焦点分别为 、 ,过 且斜率为 的直线 交椭圆 于 、 两点,则 的内切圆半径为( )A、 B、 C、 D、12. 已知方程 在 上有两个不等的实数根,则实数 的取值范围为( )A、 B、 C、 D、
A、1193 B、1359 C、2718 D、34139. 已知双曲线 , , 是双曲线上关于原点对称的两点, 是双曲线上的动点,直线 , 的斜率分别为 ,若 的最小值为2,则双曲线的离心率为( )A、 B、 C、 D、10. “三个臭皮匠,赛过诸葛亮”,这是我们常说的口头禅,主要是说集体智慧的强大. 假设李某智商较高,他独自一人解决项目M的概率为 ;同时,有 个水平相同的人也在研究项目M , 他们各自独立地解决项目M的概率都是 .现在李某单独研究项目M , 且这 个人组成的团队也同时研究项目M , 设这个 人团队解决项目M的概率为 ,若 ,则 的最小值是( )A、3 B、4 C、5 D、611. 已知椭圆 的左、右焦点分别为 、 ,过 且斜率为 的直线 交椭圆 于 、 两点,则 的内切圆半径为( )A、 B、 C、 D、12. 已知方程 在 上有两个不等的实数根,则实数 的取值范围为( )A、 B、 C、 D、二、填空题
-
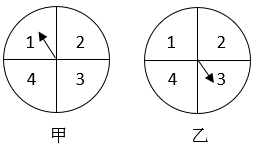
13. 已知焦点在 轴上的双曲线的渐近线方程为 ,则双曲线的离心率为.14. 同时转动如图所示的两个转盘,记转盘甲得到的数为x,转盘乙得到的数为y,构成数对(x,y),则所有数对(x,y)中满足xy=4的概率为.
 15. 在 的二项展开式中,只有第5项的二项式系数最大,则该二项展开式中的常数项等于.16. 关于曲线C: ,给出下列五个命题:
15. 在 的二项展开式中,只有第5项的二项式系数最大,则该二项展开式中的常数项等于.16. 关于曲线C: ,给出下列五个命题:①曲线C关于直线y=x对称;②曲线C关于点 对称;③曲线C上的点到原点距离的最小值为 ;④当 时,曲线C上所有点处的切线斜率为负数;⑤曲线C与两坐标轴所围成图形的面积是 .上述命题中,为真命题的是.(将所有真命题的编号填在横线上)
三、解答题
-
17. 已知函数
(I)求 在 ( 为自然对数的底数)处的切线方程.
(II)求 的最小值.
18. 已知抛物线 与直线 相交于A、B两点,点O是坐标原点.(Ⅰ)求证:;
(Ⅱ)当△OAB的面积等于 时,求t的值.
19. 如图,在四棱锥S-ABCD中, 平面 ,底面ABCD为直角梯形, , ,且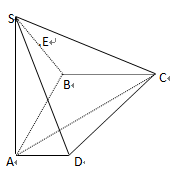
(Ⅰ)求 与平面 所成角的正弦值.
(Ⅱ)若E为SB的中点,在平面 内存在点N , 使得 平面 ,求N到直线AD , SA的距离.
20. 大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了100名魔方爱好者进行调查,得到的部分数据如表所示:已知在全部100人中随机抽取1人抽到喜欢盲拧的概率为 .喜欢盲拧
不喜欢盲拧
总计
男
10
女
20
总计
100
表(1)
并邀请这100人中的喜欢盲拧的人参加盲拧三阶魔方比赛,其完成时间的频率分布如表所示:
完成时间(分钟)
[0,10)
[10,20)
[20,30)
[30,40]
频率
0.2
0.4
0.3
0.1
表(2)
(Ⅰ)将表(1)补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为是否喜欢盲拧与性别有关?
(Ⅱ)现从表(2)中完成时间在[30,40] 内的人中任意抽取2人对他们的盲拧情况进行视频记录,记完成时间在[30,40]内的甲、乙、丙3人中恰有一人被抽到为事件A , 求事件A发生的概率.
(参考公式: ,其中 )
P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828