广西壮族自治区南宁市2018-2019学年高二下学期数学期末考试试卷
试卷更新日期:2019-07-15 类型:期末考试
一、单选题
-
1. 已知集合 , ,则 =( )A、 B、 C、 D、2. 已知 是虚数单位,则 ( )A、 B、 C、 D、3. 空气质量指数 是一种反映和评价空气质量的方法, 指数与空气质量对应如下表所示:
0~50
51~100
101~150
151~200
201~300
300以上
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
如图是某城市2018年12月全月的指 数变化统计图.
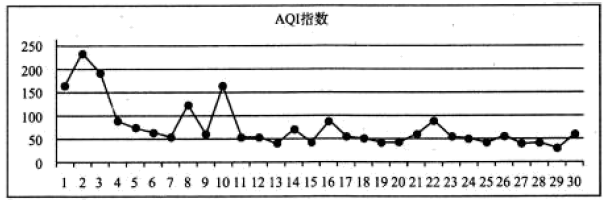
根据统计图判断,下列结论正确的是( )
A、整体上看,这个月的空气质量越来越差 B、整体上看,前半月的空气质量好于后半月的空气质量 C、从 数据看,前半月的方差大于后半月的方差 D、从 数据看,前半月的平均值小于后半月的平均值4. 若等比数列 的各项均为正数, , ,则 ( )A、 B、 C、12 D、245. 若 , 满足约束条件 ,则 的最大值为( )A、 B、 C、5 D、66. 《易经》是我国古代预测未来的著作,其中同时抛掷三枚古钱币观察正反面进行预测未知,则抛掷一次时出现两枚正面一枚反面的概率为( )A、 B、 C、 D、7. 函数 在点 处的切线方程为( )A、 B、 C、 D、8. 根据如图所示的程序框图,当输入的 值为3时,输出的 值等于( )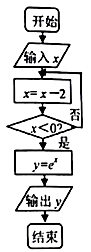 A、1 B、 C、 D、9. 下列三个数: , , ,大小顺序正确的是( )A、 B、 C、 D、10. 在空间中,给出下列说法:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面 内有不共线的三点到平面 的距离相等,则 ;④过平面 的一条斜线,有且只有一个平面与平面 垂直.其中正确的是( )A、①③ B、②④ C、①④ D、②③11. 如图,已知函数 的图象关于坐标原点对称,则函数 的解析式可能是( )
A、1 B、 C、 D、9. 下列三个数: , , ,大小顺序正确的是( )A、 B、 C、 D、10. 在空间中,给出下列说法:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面 内有不共线的三点到平面 的距离相等,则 ;④过平面 的一条斜线,有且只有一个平面与平面 垂直.其中正确的是( )A、①③ B、②④ C、①④ D、②③11. 如图,已知函数 的图象关于坐标原点对称,则函数 的解析式可能是( ) A、 B、 C、 D、12. 在平面直角坐标系 中,已知抛物线 的焦点为 ,过点 的直线 与抛物线 交于 , 两点,若 ,则 的面积为( )A、 B、 C、 D、
A、 B、 C、 D、12. 在平面直角坐标系 中,已知抛物线 的焦点为 ,过点 的直线 与抛物线 交于 , 两点,若 ,则 的面积为( )A、 B、 C、 D、二、填空题
-
13. 设向量 ,且 ,则实数 的值是;14. 已知等差数列 的前 项和为 , ;15. 若角 满足 ,则 =;16. 双曲线 的焦点是 ,若双曲线 上存在点 ,使 是有一个内角为 的等腰三角形,则 的离心率是;
三、解答题
-
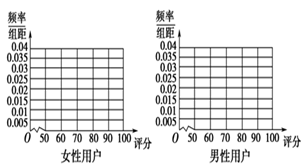
17. 三个内角A,B,C对应的三条边长分别是 ,且满足 .(1)、求角 的大小;(2)、若 , ,求 .18. 手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
女性用户
分值区间
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
20
40
80
50
10
男性用户
分值区间
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
45
75
90
60
30
参考附表:
参考公式 ,其中
(1)、完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);(2)、把评分不低于70分的用户称为“评分良好用户”,完成下列列联表,并判断能否有 的把握认为“评分良好用户”与性别有关?女性用户
男性用户
合计
“认可”手机
“不认可”手机
合计
19. 如图所示,已知ABCD是直角梯形, , .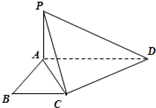 (1)、证明: ;(2)、若 ,求三棱锥 的体积.20. 已知椭圆 : 的离心率为 ,且经过点 .(1)、求椭圆 的方程;(2)、直线 与椭圆 相交于 , 两点,若 ,求 ( 为坐标原点)面积的最大值及此时直线 的方程.
(1)、证明: ;(2)、若 ,求三棱锥 的体积.20. 已知椭圆 : 的离心率为 ,且经过点 .(1)、求椭圆 的方程;(2)、直线 与椭圆 相交于 , 两点,若 ,求 ( 为坐标原点)面积的最大值及此时直线 的方程.