河南省郑州市2018-2019学年高一下学期数学期末考试试卷
试卷更新日期:2019-07-15 类型:期末考试
一、单选题
-
1. ( )A、 B、 C、 D、2. ( )A、 B、 C、 D、3. 某校高一年级从815名学生中选取30名学生参加庆祝建党98周年的大合唱节目,若采用下面的方法选取:先用简单随机抽样从815人中剔除5人,剩下的810人再按系统抽样的方法抽取,则每人入选的概率( )A、不全相等 B、均不相等 C、都相等,且为 D、都相等,且为4. 第十一届全国少数民族传统体育运动会将于2019年9月8日至16日在郑州举行.如下图所示的茎叶图是两位选手在运动会前期选拔赛中的比赛得分,则下列说法正确的是( )
 A、甲的平均数大于乙的平均数 B、甲的中位数大于乙的中位数 C、甲的方差大于乙的方差 D、甲的极差小于乙的极差5. 要得到函数 的图象,只需将函数 的图象( )A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位6. 如图给出的是计算 的值的一个程序框图,其中判断框中应填入的是( )
A、甲的平均数大于乙的平均数 B、甲的中位数大于乙的中位数 C、甲的方差大于乙的方差 D、甲的极差小于乙的极差5. 要得到函数 的图象,只需将函数 的图象( )A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位6. 如图给出的是计算 的值的一个程序框图,其中判断框中应填入的是( )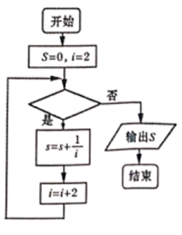 A、 B、 C、 D、7. 如图所示,在 内随机选取一点 ,则 的面积不超过四边形 面积的概率是( )
A、 B、 C、 D、7. 如图所示,在 内随机选取一点 ,则 的面积不超过四边形 面积的概率是( )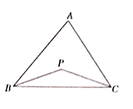 A、 B、 C、 D、8. 若 ,则 ( )A、 B、 C、 D、9. 已知边长为1的菱形 中, ,点 满足 ,则 的值是( )A、 B、 C、 D、10. 已知 , , ,则 ( )A、 B、 C、 D、11. 如图,在平行四边形 中,点 满足 , 与 交于点 ,设 ,则 ( )
A、 B、 C、 D、8. 若 ,则 ( )A、 B、 C、 D、9. 已知边长为1的菱形 中, ,点 满足 ,则 的值是( )A、 B、 C、 D、10. 已知 , , ,则 ( )A、 B、 C、 D、11. 如图,在平行四边形 中,点 满足 , 与 交于点 ,设 ,则 ( ) A、 B、 C、 D、12. 设 , ,若 对任意 成立,则下列命题中正确的命题个数是( )
A、 B、 C、 D、12. 设 , ,若 对任意 成立,则下列命题中正确的命题个数是( )⑴ ;⑵ ;⑶ 不具有奇偶性(4) 的单调增区间是 (5)可能存在经过点 的直线与函数的图象不相交
A、1个 B、2个 C、3个 D、4个二、填空题
-
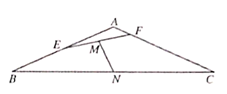
13. 平面向量 的夹角为 ,若 , ,则14. 在 中, ,则 等于 .15. 水痘是一种传染性很强的病毒性疾病,易在春天爆发.市疾控中心为了调查某校高一年级学生注射水症疫苗的人数,在高一年级随机抽取5个班级,每个班抽取的人数互不相同,若把每个班级抽取的人数作为样本数据.已知样本平均数为7,样本方差为4,则样本数据中的最大值是 .16. 如图在 中,已知 , , 分别是边 上的点,且 , ,其中 ,且 ,若线段 的中点分别为 ,则 的最小值为 .
三、解答题
-
17. 已知平面向量 ,
(I)若 ,求 ;
(Ⅱ)若 ,求 与 所成夹角的余弦值.
18. 如图所示,在平面直角坐标系中,角 与 ( )的顶点与坐标原点重合,始边与 轴的非负半轴重合,终边分别与单位圆交于 两点,点 的横坐标为 .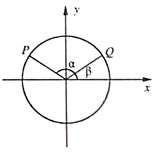
(I)求 ;
(Ⅱ)若 ,求 .
19. 2019年5月5日6时许,桂林市雁山区一出租房发生一起重大火灾,事故发生后,附近消防员及时赶到,控制住火情,将灾难损失降到了最低.某保险公司统计的数据表明:居民住宅区到最近消防站的距离 (单位:千米)和火灾所造成的损失数额 (单位:千元)有如下的统计资料:距消防站距离 (千米)
1.8
2.6
3.1
4.3
5.5
6.1
火灾损失费用 (千元)
17.8
19.6
27.5
31.3
36.0
43.2
如果统计资料表明 与 有线性相关关系,试求(解答过程中,各种数据都精确到0.01)
(I)相关系数 ;
(Ⅱ)线性回归方程;
(Ⅲ)若发生火灾的某居民区与最近的消防站相距10.0千米,评估一下火灾的损失.
参考数据: , , ,
参考公式:相关系数
回归方程 中斜率和截距的最小二乘法估计公式分别为: , .
20. 已知函数 的部分图象如图所示:
(I)求 的解析式及对称中心坐标;
(Ⅱ)将 的图象向右平移 个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数 的图象,求函数 在 上的单调区间及最值.
21. 近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中 .
(I)求 的值;
(Ⅱ)求被调查的市民的满意程度的平均数,众数,中位数;
(Ⅲ)若按照分层抽样从 , 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在 的概率.
22. 已知向量 , 且函数 的两个对称中心之间的最小距离为 .(I)求 的解析式及 的值;
(Ⅱ)若函数 在 上恰有两个零点,求实数 的取值范围.