广西梧州市2019年中考数学试卷
试卷更新日期:2019-07-15 类型:中考真卷
一、选择题(本大题共12小题,每小题3分,共36分.)
-
1. ﹣6的倒数是( )A、﹣6 B、6 C、 D、2. 下列计算正确的是( )A、3x﹣x=3 B、2x+3x=5x2 C、(2x)2=4x2 D、(x+y)2=x2+y23. 一个几何体的主视图和左视图都是矩形,俯视图是圆,则这个几何体是( )A、圆柱 B、圆锥 C、球 D、正方体4. 下列函数中,正比例函数是( )A、y=﹣8x B、y= C、y=8x2 D、y=8x﹣45. 如图,钟表上10点整时,时针与分针所成的角是( )
 A、30° B、60° C、90° D、120°6. 直线y=3x+1向下平移2个单位,所得直线的解析式是( )A、y=3x+3 B、y=3x﹣2 C、y=3x+2 D、y=3x﹣17. 正九边形的一个内角的度数是( )A、108° B、120° C、135° D、140°8. 如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( )
A、30° B、60° C、90° D、120°6. 直线y=3x+1向下平移2个单位,所得直线的解析式是( )A、y=3x+3 B、y=3x﹣2 C、y=3x+2 D、y=3x﹣17. 正九边形的一个内角的度数是( )A、108° B、120° C、135° D、140°8. 如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( )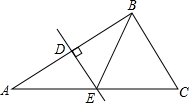 A、12 B、13 C、14 D、159. 不等式组 的解集在数轴上表示为( )A、
A、12 B、13 C、14 D、159. 不等式组 的解集在数轴上表示为( )A、 B、
B、 C、
C、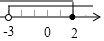 D、
D、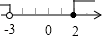 10. 某校九年级模拟考试中,1班的六名学生的数学成绩如下:96,108,102,110,108,82.下列关于这组数据的描述不正确的是( )A、众数是108 B、中位数是105 C、平均数是101 D、方差是9311. 如图,在半径为 的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )
10. 某校九年级模拟考试中,1班的六名学生的数学成绩如下:96,108,102,110,108,82.下列关于这组数据的描述不正确的是( )A、众数是108 B、中位数是105 C、平均数是101 D、方差是9311. 如图,在半径为 的⊙O中,弦AB与CD交于点E,∠DEB=75°,AB=6,AE=1,则CD的长是( )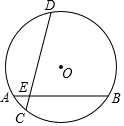 A、2 B、2 C、2 D、412. 已知m>0,关于x的一元二次方程(x+1)(x﹣2)﹣m=0的解为x1 , x2(x1<x2),则下列结论正确的是( )A、x1<﹣1<2<x2 B、﹣1<x1<2<x2 C、﹣1<x1<x2<2 D、x1<﹣1<x2<2
A、2 B、2 C、2 D、412. 已知m>0,关于x的一元二次方程(x+1)(x﹣2)﹣m=0的解为x1 , x2(x1<x2),则下列结论正确的是( )A、x1<﹣1<2<x2 B、﹣1<x1<2<x2 C、﹣1<x1<x2<2 D、x1<﹣1<x2<2二、填空题(本大题共6小题,每小题3分,共18分.)
-
13. 计算: = .14. 如图,已知在△ABC中,D、E分别是AB、AC的中点,F、G分别是AD、AE的中点,且FG=2cm,则BC的长度是cm.
 15. 化简: ﹣a=.16. 如图,▱ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF=度.
15. 化简: ﹣a=.16. 如图,▱ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF=度.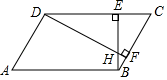 17. 如图,已知半径为1的⊙O上有三点A、B、C,OC与AB交于点D,∠ADO=85°,∠CAB=20°,则阴影部分的扇形OAC面积是.
17. 如图,已知半径为1的⊙O上有三点A、B、C,OC与AB交于点D,∠ADO=85°,∠CAB=20°,则阴影部分的扇形OAC面积是.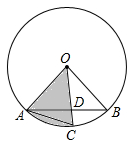 18. 如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是.
18. 如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是.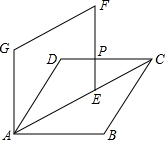
三、解答题(本大题共8小题,满分66分.)
-
19. 计算:﹣5×2+3÷ ﹣(﹣1).20. 先化简,再求值: ﹣ ,其中a=﹣2.21. 解方程: +1= .22. 一个不透明的口袋中有三个完全相同的小球,球上分别标有数字﹣1,1,2.第一次从袋中任意摸出一个小球(不放回),得到的数字作为点M的横坐标x;再从袋中余下的两个小球中任意摸出一个小球,得到的数字作为点M的纵坐标y.(1)、用列表法或树状图法,列出点M(x,y)的所有可能结果;(2)、求点M(x,y)在双曲线y=﹣ 上的概率.23. 如图,在Rt△ABC中,∠C=90°,D为BC上一点,AB=5,BD=1,tanB= .
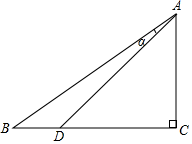 (1)、求AD的长;(2)、求sinα的值.24. 我市某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为x元/件(x≥6,且x是按0.5元的倍数上涨),当天销售利润为y元.(1)、求y与x的函数关系式(不要求写出自变量的取值范围);(2)、要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)、若每件文具的利润不超过80%,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.25. 如图,在矩形ABCD中,AB=4,BC=3,AF平分∠DAC,分别交DC,BC的延长线于点E,F;连接DF,过点A作AH∥DF,分别交BD,BF于点G,H.
(1)、求AD的长;(2)、求sinα的值.24. 我市某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为x元/件(x≥6,且x是按0.5元的倍数上涨),当天销售利润为y元.(1)、求y与x的函数关系式(不要求写出自变量的取值范围);(2)、要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)、若每件文具的利润不超过80%,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.25. 如图,在矩形ABCD中,AB=4,BC=3,AF平分∠DAC,分别交DC,BC的延长线于点E,F;连接DF,过点A作AH∥DF,分别交BD,BF于点G,H. (1)、求DE的长;(2)、求证:∠1=∠DFC.26. 如图,已知⊙A的圆心为点(3,0),抛物线y=ax2﹣ x+c过点A,与⊙A交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
(1)、求DE的长;(2)、求证:∠1=∠DFC.26. 如图,已知⊙A的圆心为点(3,0),抛物线y=ax2﹣ x+c过点A,与⊙A交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1. (1)、请直接写出点B的坐标,并求a、c的值;(2)、直线y=kx+1经过点B,与x轴交于点D.点E(与点D不重合)在该直线上,且AD=AE,请判断点E是否在此抛物线上,并说明理由;(3)、如果直线y=k1x﹣1与⊙A相切,请直接写出满足此条件的直线解析式.
(1)、请直接写出点B的坐标,并求a、c的值;(2)、直线y=kx+1经过点B,与x轴交于点D.点E(与点D不重合)在该直线上,且AD=AE,请判断点E是否在此抛物线上,并说明理由;(3)、如果直线y=k1x﹣1与⊙A相切,请直接写出满足此条件的直线解析式.