广西贺州市2019年中考数学试卷
试卷更新日期:2019-07-15 类型:中考真卷
一、选择题:(本大题共12小题,每小题3分,共36分.)
-
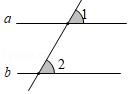
1. ﹣2的绝对值是( )A、﹣2 B、2 C、 D、﹣2. 如图,已知直线a∥b,∠1=60°,则∠2的度数是( )
 A、45° B、55° C、60° D、120°3. 一组数据2,3,4,x,6的平均数是4,则x是( )A、2 B、3 C、4 D、54. 如图是某几何体的三视图,则该几何体是( )
A、45° B、55° C、60° D、120°3. 一组数据2,3,4,x,6的平均数是4,则x是( )A、2 B、3 C、4 D、54. 如图是某几何体的三视图,则该几何体是( ) A、长方体 B、正方体 C、三棱柱 D、圆柱5. 某图书馆有图书约985000册,数据985000用科学记数法可表示为( )A、985×103 B、98.5×104 C、9.85×105 D、0.985×1066. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、正三角形 B、平行四边形 C、正五边形 D、圆7. 如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( )
A、长方体 B、正方体 C、三棱柱 D、圆柱5. 某图书馆有图书约985000册,数据985000用科学记数法可表示为( )A、985×103 B、98.5×104 C、9.85×105 D、0.985×1066. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、正三角形 B、平行四边形 C、正五边形 D、圆7. 如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( ) A、5 B、6 C、7 D、88. 把多项式4a2﹣1分解因式,结果正确的是( )A、(4a+1)(4a﹣1) B、(2a+1)(2a﹣1) C、(2a﹣1)2 D、(2a+1)29. 已知方程组 ,则2x+6y的值是( )A、﹣2 B、2 C、﹣4 D、410. 已知ab<0,一次函数y=ax﹣b与反比例函数y= 在同一直角坐标系中的图象可能( )A、
A、5 B、6 C、7 D、88. 把多项式4a2﹣1分解因式,结果正确的是( )A、(4a+1)(4a﹣1) B、(2a+1)(2a﹣1) C、(2a﹣1)2 D、(2a+1)29. 已知方程组 ,则2x+6y的值是( )A、﹣2 B、2 C、﹣4 D、410. 已知ab<0,一次函数y=ax﹣b与反比例函数y= 在同一直角坐标系中的图象可能( )A、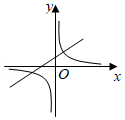 B、
B、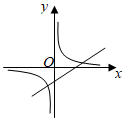 C、
C、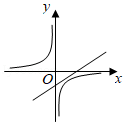 D、
D、 11. 如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半径的⊙O与AC相切于点D,BD平分∠ABC,AD= OD,AB=12,CD的长是( )
11. 如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半径的⊙O与AC相切于点D,BD平分∠ABC,AD= OD,AB=12,CD的长是( )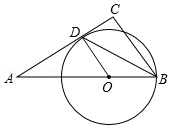 A、2 B、2 C、3 D、412. 计算 + + + +…+ 的结果是( )A、 B、 C、 D、
A、2 B、2 C、3 D、412. 计算 + + + +…+ 的结果是( )A、 B、 C、 D、二、填空题:(本大题共6小题,每小题3分,共18分.)
-
13. 要使分式 有意义,则x的取值范围是.14. 计算a3•a的结果是.15. 调查我市一批药品的质量是否符合国家标准.采用方式更合适.(填“全面调查”或“抽样调查”)16. 已知圆锥的底面半径是1,高是 ,则该圆锥的侧面展开图的圆心角是度.17. 已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,其部分图象如图所示,下列说法中:①abc<0;②a﹣b+c<0;③3a+c=0;④当﹣1<x<3时,y>0,正确的是(填写序号).
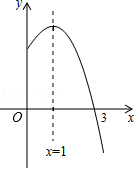 18. 如图,正方形ABCD的边长为4,点E是CD的中点,AF平分∠BAE交BC于点F,将△ADE绕点A顺时针旋转90°得△ABG,则CF的长为.
18. 如图,正方形ABCD的边长为4,点E是CD的中点,AF平分∠BAE交BC于点F,将△ADE绕点A顺时针旋转90°得△ABG,则CF的长为.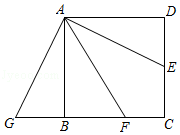
三、解答题:(本大题共8题,满分66分.)
-
19. 计算:(﹣1)2019+(π﹣3.14)0﹣ +2sin30°.20. 解不等式组:21. 箱子里有4瓶牛奶,其中有一瓶是过期的.现从这4瓶牛奶中不放回地任意抽取2瓶.(1)、请用树状图或列表法把上述所有等可能的结果表示出来;(2)、求抽出的2瓶牛奶中恰好抽到过期牛奶的概率.22. 如图,在A处的正东方向有一港口B.某巡逻艇从A处沿着北偏东60°方向巡逻,到达C处时接到命令,立刻在C处沿东南方向以20海里/小时的速度行驶3小时到达港口B.求A,B间的距离.( ≈1.73, ≈1.4,结果保留一位小数).
 23. 2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.(1)、求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;(2)、若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?24. 如图,在矩形ABCD中,E,F分别是BC,AD边上的点,且AE=CF.
23. 2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.(1)、求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;(2)、若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?24. 如图,在矩形ABCD中,E,F分别是BC,AD边上的点,且AE=CF. (1)、求证:△ABE≌△CDF;(2)、当AC⊥EF时,四边形AECF是菱形吗?请说明理由.
(1)、求证:△ABE≌△CDF;(2)、当AC⊥EF时,四边形AECF是菱形吗?请说明理由.