浙江省台州市天台县2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2019-07-15 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分。）

1. $\sqrt{2}$ 的相反数是（）

A、 $2$ B、 $0$ C、 $\sqrt{2}$ D、 $- \sqrt{2}$

查看试题解析
2. 如图，直线 $a$ //b，下列各角中与 $∠ 1$ 相等的是（）

A、 $∠ 2$ B、 $∠ 3$ C、 $∠ 4$ D、 $∠ 5$

查看试题解析
3. 关于 $x$ 的不等式组的解集在数轴上表示如图所示，则不等式组解集为（）

A、 $- 2 \leq x \leq 1$ B、 $- 2 \leq x < 1$ C、 $- 2 < x \leq 1$ D、 $- 2 < x < 1$

查看试题解析
4. 如图，在三角形ABC和三角形ABD中，∠ABC=∠ADB=90°，则边AC，AB，CB，AD中最长的是（）

A、 $A C$ B、 $A B$ C、 $B C$ D、 $A D$

查看试题解析
5. 若 $a > b$ ，则下列式子中错误的是（）

A、 $a - 1 > b - 1$ B、 $2 a > 2 b$ C、 $\frac{a}{3} > \frac{b}{3}$ D、 $- 3 a > - 3 b$

查看试题解析
6. 下列各数中最大的是（）

A、 $2 - \sqrt{5}$ B、1 C、 $\sqrt{5} - 2$ D、 $3 - \sqrt{5}$

查看试题解析
7. 把平面直角坐标系中的一点 $P$ ( $3$ ， $m$ )向上平移2个单位长度后，点P的对应点P′刚好落在x轴上，则 $m$ 的值为（）

A、 $- 2$ B、0 C、 $1$ D、 $2$

查看试题解析
8. 为了调查某校学生的视力情况，在全校的800名学生中随机抽取了80名学生，下列说法正确的是（）

A、此次调查属于全面调查 B、样本容量是80 C、800名学生是总体 D、被抽取的每一名学生称为个体

查看试题解析
9. 已知 $\min {\sqrt{x}$ ， $x^{2}$ ， $x}$ 表示取三个数中最小的那个数﹒例如：当 $x = 9$ ， $\min {\sqrt{x}$ ， $x^{2}$ ， $x}$ = $\min {\sqrt{9}$ ， $9^{2}$ ， $9}$ =3﹒当 $\min {\sqrt{x}$ ， $x^{2}$ ， $x}$ = $\frac{1}{16}$ 时，则 $x$ 的值为（）

A、 $\frac{1}{16}$ B、 $\frac{1}{8}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
10. 如图1，当光线在空气进入水中时，会发生折射，满足入射角 $∠ 1$ 与折射角 $∠ 2$ 的度数比为 $4 ： 3$ ﹒如图2，在同一平面上，两条光线同时从空气进入水中，两条入射光线与水面夹角分别为 $α$ ， $β$ ，在水中两条折射光线的夹角为 $γ$ ，则 $α$ ， $β$ ， $γ$ 三者之间的数量关系为（）

A、 $\frac{3}{4} (α + β) = γ$ B、 $\frac{3}{4} (α + β) = 135 ° - γ$ C、 $α + β = γ$ D、 $α + β + γ = 180 °$

查看试题解析

二、填空题（本题有6小题，每小题3分，共18分）

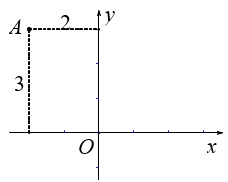
11. 实数3的算术平方根是．

查看试题解析
12. 如图，平面直角坐标系内，有一点A到x轴的距离为3，到y轴的距离为2，则点A的坐标为．

查看试题解析
13. 古代算筹图用图1表示方程组： ${\begin{matrix} 4 x + 7 y = 72 \\ 6 x + 3 y = 44 \end{matrix}$ ，请写出图2所表示的二元一次方程组．

查看试题解析
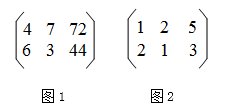14. 小明将同学们周末生活的调查结果绘制成了扇形统计图.其中，看书这一项对应的圆心角度数为72°，则周末看书的同学人数占了总数的． ( 填百分比 )

查看试题解析
15. 已知关于x，y的方程组 ${\begin{cases} x + 2 y = k \\ 2 x + 3 y = 3 k - 1 \end{cases}$ ，有以下结论：①当k=0时，方程组的解是 ${\begin{matrix} x = - 2 \\ y = 1 \end{matrix}$ ；
②方程组的解可表示为 ${\begin{matrix} x = 3 k - 2 \\ y = 1 - k \end{matrix}$ ；③不论k取什么实数， $x + 3 y$ 的值始终不变.

其中正确的有．（填写编号）

查看试题解析
16. 极坐标系也可用来确定点的位置﹒如图，过平面内一点O，作一条射线Ox，点M的极坐标就可以用线段OM的长度以及Ox转动到OM的角度 $θ$ （规定取逆时针方向为角的正方向， $0^{°} \leq θ \leq 360 °$ ）来确定﹒已知OM=3， $θ = 45 °$ ，点M的极坐标表示为（3，45°），平面内现有一点N，满足∠MON=90°，ON=OM，则点N的极坐标可以表示为．

查看试题解析

三、解答题（本题有8小题，第17～21题每题8分, 第22～23题每题10分, 第24题12分，共72分）

17.

(1)、计算： $2 - \sqrt[3]{8}$ ；

(2)、解不等式组： ${\begin{cases} x + 1 > 3, \\ 5 x - 2 \leq 3 (x + 1) . \end{cases}$

查看试题解析
18. 完成下面的证明：
如图，∠C=50°，E是BA延长线上的一点，过点A作 $A D$ //BC﹒若AD平分∠CAE，求∠B的度数．

解：∵ $A D$ //BC，∠C=50°（已知），

∴∠2==°（）.

又∵AD平分∠CAE（已知），

∴=∠2=50°（）.

又∵ $A D$ //BC（已知），

∴∠B==°（）.

查看试题解析
19. 课本里，用代入法解二元一次方程组 ${\begin{matrix} x - y = 2 \\ 2 x + y = 7 \end{matrix}$ 的过程是用下面的框图表示：
根据以上思路，请用代入法求出方程组 ${\begin{matrix} x - y = 0 \\ | x - 2 y | = 2 \end{matrix}$ 的解（不用画框架图）.

查看试题解析
20. 某校为了迎接体育中考，3月底对初三某班学生进行了一次跳绳测试，测试成绩分别记为A，B，C，D，E共5个等级（其中D，E为优良），并绘制成了统计图1.在进行了为期一个月的特训后，4月底对同一批学生又进行了一次跳绳测试，发现A类的人数没有发生变化，并将成绩绘制成统计图2.请根据图中提供的信息，解答下列问题：

(1)、求此次参加测试的学生人数；

(2)、补全频数分布直方图和扇形统计图；

(3)、请估计该校九年级500名学生在进行一个月的特训后，优良人数增加了多少.

查看试题解析
21. 如图，已知 $∠ 1 + ∠ 2 = 180 °$ ， $∠ A C B = ∠ A E D$ .求证：∠B=∠3.

查看试题解析

22. 一个运输公司有甲、乙两种货车，两次满载的运输情况如下表：

	甲种货车辆数	乙种货车辆数	合计运货吨数
第一次	2	4	18
第二次	5	6	35

(1)、求甲、乙两种货车每次满载分别能运输多少吨货物；

(2)、现有一批重34吨的货物需要运输，而甲、乙两种货车运输的保养费用分别为80元/辆和40元/辆.公司打算由甲、乙两种货车共10辆来完成这次运输，为了使保养费用不超过700元，公司该如何安排甲、乙两种货车来完成这次运输任务.

查看试题解析

23. 如图，在平面直角坐标系中，把二元一次方程 $x + y = 4$ 的若干个解用点表示出来，发现它们都落在同一条直线上.一般地，任何一个二元一次方程的所有解用点表示出来，它的图象就是一条直线.根据这个结论，解决下列问题：

(1)、根据图象判断二元一次方程 $x + y = 4$ 的正整数解为；(写出所有正整数解)

(2)、若在直线上取一点 $M$ ( $1$ ， $3$ )，先向下平移 $a$ 个单位长度，再向右平移 $b$ 个单位长度得到点M′，发现点M′又重新落在二元一次方程 $x + y = 4$ 的图象上，试探究 $a$ ， $b$ 之间满足的数量关系.

查看试题解析
24. 如图1，教材P₄₁页有这样一个探究：把两个边长为1dm的小正方形分别沿对角线剪开，将所得的4个直角三角形拼在一起，就可以得到一个面积为2dm²的大正方形．试根据这个研究方法回答下列问题：

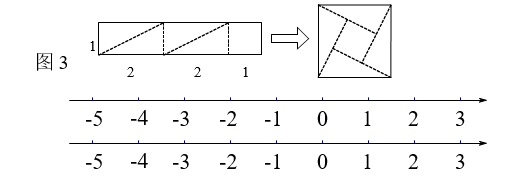(1)、所得到的面积为2dm²的大正方形的边就是原先边长为1dm的小正方形的对角线长，因此，可得小正方形的对角线长为；

(2)、由此，我们得到了一种方法，能在数轴上画出无理数所对应的点，则图2中 $A$ ， $B$ 两点表示的数分别为，；

(3)、通过动手操作，小张同学把长为5，宽为1的长方形进行裁剪，拼成如图3所示的一个正方形．请用（2）中相同的方法在两条数轴上分别找到表示 $\sqrt{5}$ 以及 $\sqrt{5} - 3$ 的点．（作图过程中标出必要线段长）

查看试题解析