浙江省台州市天台县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2019-07-15 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题，每小题4分，共40分．）

1. 下列三条线段能构成直角三角形的是（）

A、6, 7, 8 B、2, 3, 4 C、3, 4, 6 D、6，8, 10

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{12} = 2 \sqrt{3}$ B、 $3 \sqrt{3} - \sqrt{3} = 3$ C、 $2 + \sqrt{3} = 2 \sqrt{3}$ D、 $\sqrt{{(- 2)}^{2}} = - 2$

查看试题解析
3. 下列关系不是函数关系的是（）

A、汽车在匀速行驶过程中，油箱的余油量y（升）是行驶时间t（小时）的函数 B、改变正实数x ，它的平方根y随之改变，y是x的函数 C、电压一定时，通过某电阻的电流强度I(单位：安)是电阻R（单位:欧姆）的函数 D、垂直向上抛一个小球，小球离地的高度h（单位：米）是时间t（单位：秒）的函数

查看试题解析
4. 如图，在菱形 $A B C D$ 中，E ， F分别是 $A B ， A C$ 的中点，若∠B=50°，则∠AFE的度数为（）

A、50° B、60° C、65° D、70°

查看试题解析

5. 下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差：

	甲	乙	丙	丁
平均数（分）	92	95	95	92
方差	3.6	3.6	7.4	8.1

要选择一名成绩好且发挥稳定的同学参加数学竞赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

6. 矩形不一定具有的性质是（）

A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、是轴对称图形

查看试题解析
7. 如图，△ABC中，D ， E分别是AB ， AC的中点，点F在DE上，且∠AFB＝90°，若AB＝5，BC＝8，则EF的长为（）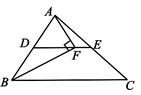

A、2.5 B、2 C、1.5 D、1

查看试题解析
8. 如图，在一张平行四边形纸片ABCD中，画一个菱形，甲、乙两位同学的画法如下：
甲：以B ， A为圆心，AB长为半径作弧，分别交BC ， AD于点E ， F ，则四边形ABEF为菱形；乙：作∠A ， ∠B的平分线AE ， BF ，分别交BC于点E ，交AD于点F ，则四边形ABEF是菱形；关于甲、乙两人的画法，下列判断正确的是（）

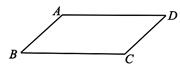A、仅甲正确 B、仅乙正确 C、甲、乙均正确 D、甲、乙均错误

查看试题解析
9. 如图，已知矩形纸片ABCD的两边AB：BC=2：1，过点B折叠纸片，使点A落在边CD上的点F处，折痕为BE ．若AB的长为4，则EF的长为（）

A、 $8 - 4 \sqrt{3}$ B、 $2 \sqrt{3}$ C、 $4 \sqrt{3} - 6$ D、 $\frac{6}{5}$

查看试题解析
10. 小明从家出发，沿一条直道跑步，经过一段时间原路返回，刚好在第16分钟回到家中. 设小明出发第 $t$ 分钟的速度为 $v$ 米/分，离家的距离为 $s$ 米. $v$ 与 $t$ 之间的部分图象、 $s$ 与 $t$ 之间的部分图象分别如图1与图2（图象没画完整，其中图中的空心圈表示不包含这一点），则当小明离家600米时，所用的时间是（）分钟.

A、4.5 B、8.25 C、4.5 或8.25 D、4.5 或 8.5

查看试题解析

二、填空题（本题有6小题，每小题5分，共30分）

11. 若二次根式 $\sqrt{a - 2}$ 有意义，则 $a$ 的取值范围是.

查看试题解析
12. 如果点A（1，m）在直线 $y = - 2 x + 1$ 上，那么m= ．

查看试题解析
13. 若 x= $\sqrt{3} + 1$ ，y= $\sqrt{3} - 1$ ，则 x²-y² =.

查看试题解析
14. 如图，E是 $▱$ ABCD边BC上一点，连结AE ，并延长AE与DC的延长线交于点F ，若AB=AE ， ∠F =50°，则∠D=°．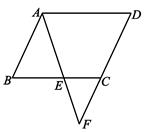

查看试题解析
15. 已知，点O为数轴原点，数轴上的A ， B两点分别对应 $- 3$ ， $3$ ，以AB为底边作腰长为4的等腰△ABC ，连接OC ，以O为圆心，CO长为半径画弧交数轴于点M ，则点M对应的实数为.

查看试题解析
16. 如图，四边形ABCD为菱形，∠D=60°，AB=4，E为边BC上的动点，连接AE ，作AE的垂直平分线GF交CD于F点，垂足为点G，则线段GF 的最小值为.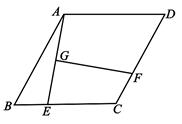

查看试题解析

三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22，23题每题12分，第24题14分，共80分）

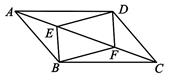
17. 计算： $\sqrt{2} \times (\sqrt{18} - \sqrt{\frac{1}{2}})$ ．

查看试题解析
18. 如图，在 $▱$ ABCD中，E ， F是对角线AC上的两点，且AF=CE.
求证： DE∥BF.

查看试题解析
19. 平面直角坐标系 $x O y$ 中，直线 $y = \frac{3}{2} x + b$ 与直线 $y = \frac{1}{2} x$ 交于点 $A (m, 1)$ ，与 $y$ 轴交于点 $B$ .

(1)、求 $m$ 的值和点 $B$ 的坐标；

(2)、若点 $C$ 在 $y$ 轴上，且△ $A B C$ 的面积是1，请直接写出点 $C$ 的坐标．

查看试题解析
20. 如图，正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫格点．

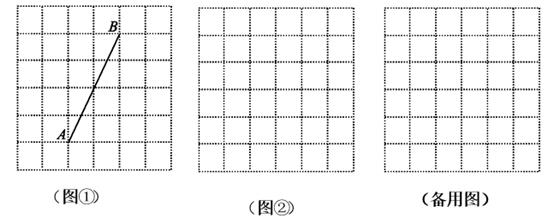(1)、在图①中，求线段AB的长度；若在图中画出以C为直角顶点的Rt△ABC ，使点C在格点上，请在图中画出所有点C；

(2)、在图②中，以格点为顶点，请先用无刻度的直尺画正方形ABCD ，使它的面积为13；再画一条直线PQ（不与正方形对角线重合），使PQ恰好将正方形ABCD的面积二等分(保留作图痕迹）.

查看试题解析
21. 某工厂为了解甲、乙两个部门员工的生产技能情况，从甲、乙两个部门各随机抽取20名员工，进行生产技能测试，测试成绩（百分制）如下：
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77

乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40

（说明：成绩80分及以上为优秀，70—79分为良好，60—69分为合格，60分以下为不合格）

(1)、请填完整表格：

部门

平均数

中位数

众数

甲

78.3

75

乙

78

80.5

(2)、从样本数据可以推断出哪个部门员工的生产技能水平较高，请说明理由．
（至少从两个不同的角度说明推断的合理性）.

查看试题解析
22. 计算 $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} + \dots + \sqrt{1 + \frac{1}{1001^{2}} + \frac{1}{1002^{2}}}$ .

(1)、研究规律：先观察几个具体的式子：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = \sqrt{\frac{9}{4}} = \frac{3}{2} = \frac{2}{1} -$ 。
$\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = \sqrt{\frac{49}{36}} = \frac{7}{6} = \frac{3}{2} -$ 。
$\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = \sqrt{\frac{169}{144}} = \frac{13}{12} =$ 。

(2)、寻找规律：
$\sqrt{1 + \frac{1}{n^{2}} + \frac{1}{{(n + 1)}^{2}}} =$ $(n \geq 1 且 n 为正整数)$

(3)、请完成计算：
$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} + \dots + \sqrt{1 + \frac{1}{1001^{2}} + \frac{1}{1002^{2}}}$

查看试题解析
23. 如图

(1)、如图1，观察函数 $y = | x |$ 的图象，写出它的两条的性质；

(2)、在图1中，画出函数 $y = | x - 3 |$ 的图象；
根据图象判断：函数 $y = | x - 3 |$ 的图象可以由 $y = | x |$ 的图象向平移个单位得到；

(3)、①函数 $y = | 2 x + 3 |$ 的图象可以由 $y = | 2 x |$ 的图象向平移单位得到；
②根据从特殊到一般的研究方法，函数 $y = | k x + 3 |$ （ $k$ 为常数， $k$ ≠0）的图象可以由函数 $y = | k x |$ （ $k$ 为常数， $k$ ≠0）的图象经过怎样的平移得到.

查看试题解析
24. 如图1，在正方形ABCD中，点E ， F分别是AC ， BC上的点，且满足DE ⊥EF ，垂足为点E ，连接DF.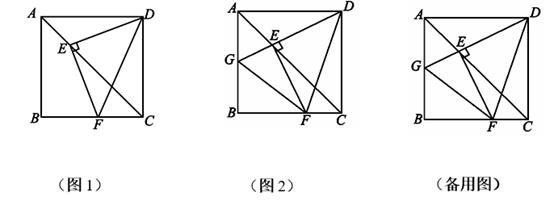

(1)、求∠EDF=(填度数)；

(2)、延长DE交AB于点G ，连接FG ，如图2，猜想AG ， GF ， FC三者的数量关系，并给出证明；

(3)、①若AB=6，G 是AB 的中点，求△BFG的面积；
②设AG = $a$ ，CF = $b$ ，△BFG 的面积记为S ，试确定S与 $a$ ， $b$ 的关系，并说明理由.

查看试题解析

部门	平均数	中位数	众数
甲	78.3		75
乙	78	80.5