浙江省丽水市莲都区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2019-07-15 类型：期末考试

进入出卷网下载

一、选择题（本题有10小题,每小题3分,共30分.）

1. 要使式子 $\sqrt{x - 4}$ 有意义,则x可取的数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 下列各点中,在反比例函数y＝ $\frac{- 6}{x}$ 图象上的点是（）

A、(1,6) B、(2,3) C、(－2,－3) D、(－3,2)

查看试题解析
3. 用反证法证明“a＞b”时,应先假设（）

A、a≥b B、a≤b C、a=b D、a＜b

查看试题解析
4. 如图，在四边形ABCD中，AC与BD相交于点O ，下列条件不能判定四边形ABCD为平行四边形的是（）

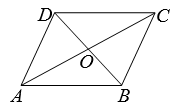A、AB∥DC ， AB=DC B、AB=DC ， AD=BC C、AB∥DC ， AD=BC D、OA=OC ， OB=OD

查看试题解析

5. 某射击队要从甲,乙,丙,丁四名队员中选出一名队员代表射击队参加射击比赛,各队员的平时成绩的平均数及方差如表所示:

	甲	乙	丙	丁
平均数(环)	9.8	9.3	9.6	9.8
方差(环²)	3.3	3.3	3.5	6.1

根据表中数据,要从这四个队员中选择一个成绩好且发挥稳定的队员去参赛,那么应该选的队员是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

6. 用配方法解一元二次方程x²－8x＋3＝0时,可将方程化为（）

A、(x－8)²＝13 B、(x＋4)²＝13 C、(x－4)²＝13 D、(x＋4)²＝19

查看试题解析
7. 已知A(1,y₁),B(2,y₂),C(－3,y₃)都在反比例函数 $y = \frac{k}{x}$ (k＞0)的图象上,则y₁,y₂,y₃的大小关系是（）

A、y₂＞y₁＞y₃ B、y₁＞y₂＞y₃ C、y₃＞y₂＞y₁ D、y₁＞y₃＞y₂

查看试题解析
8. 已知直角三角形的两条直角边长恰好是方程x²－5x＋6＝0的两个根,则此直角三角形斜边长是（）

A、 $\sqrt{13}$ B、 $\sqrt{5}$ C、13 D、5

查看试题解析
9. 将矩形ABCD按如图方式折叠，点B ，点C恰好落在点G处，且A ， G ， F在同一条直线上．若AB=4，BC=6，则CF的长是（）

A、 $\frac{9}{4}$ B、 $\frac{5}{2}$ C、 $\frac{11}{4}$ D、3

查看试题解析
10. 关于x的方程 $m^{2} x^{2} - 8 m x + 12 = 0$ 至少有一个正整数解,且m是整数,则满足条件的m的值的个数是（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题（本题有6小题,每小题3分,共18分）

11. 计算： $\sqrt{{(- 4)}^{2}}$ = ．

查看试题解析
12. 已知一个多边形的每个内角都为140°,则这个多边形的边数是．

查看试题解析
13. 一组数据：8,1,4,3,x的平均数为x,则这组数据的众数是．

查看试题解析
14. 设函数 $y = \frac{- 2}{x}$ 与y=x＋4的图象的交点坐标为(a,b),则 $\frac{1}{a} - \frac{1}{b}$ 的值是．

查看试题解析
15. 现要在一个长为40m，宽为26m的矩形花园中修建等宽的小道，剩余的地方种植花草.如图所示，要使种植花草的面积为864m² ，那么小道的宽度应是m．

查看试题解析
16. 如图，已知线段 AC=4，线段BC绕点C旋转，且BC=6，连结AB ，以AB为边作正方形ADEB ，连结CD.

(1)、若∠ACB=90°，则AB的值是；

(2)、线段CD长的最大值是．

查看试题解析

三、解答题(本题有8小题,共52分)

17. 计算

(1)、 ${(\sqrt{8})}^{2} - 2 \sqrt{4}$ ；

(2)、 $\sqrt{6} \times \sqrt{3} \div \frac{2}{\sqrt{2}}$ .

查看试题解析
18. 解方程

(1)、7x²－49x＝0；

(2)、x²－2x－1＝0.

查看试题解析

19. 某中学随机抽取部分学生进行科技知识的调查测试，测试成绩分为A，B，C，D，E五个等级，通过对测试成绩的分析，得到如下条形统计图：

等级	成绩
A	50≤x＜60
B	60≤x＜70
C	70≤x＜80
D	80≤x＜90
E	90≤x＜100

请根据所给信息，解答下列问题：

(1)、试分析本次调查测试成绩的“中位数”在哪个等级；

(2)、若本次调查测试成绩在80分及以上为优秀，该中学共有800人，请估计全校测试成绩为优秀的学生人数.

查看试题解析

20. 已知在平面直角坐标系中，一次函数y＝x+b的图象与反比例函数y＝ $\frac{k}{x}$ 的图象交于点A(1，m)和点B(－2，－1)

(1)、求k ， b的值；

(2)、连结OA ， OB ，求△AOB的面积.

查看试题解析
21. 如图，在矩形ABCD中，∠BAD的平分线交BC于点E ，交DC的延长线于点F.

(1)、若AB=2，AD=3，求EF的长；

(2)、若G是EF的中点，连接BG和DG ，
求证：DG=BG.

查看试题解析
22. 某商场销售一批鞋子,平均每天可售出20双,每双盈利50元.为了扩大销售,增加盈利,商场决定采取降价措施,调查发现,每双鞋子每降价1元,商场平均每天可多售出2双．

(1)、若每双鞋子降价20元,商场平均每天可售出多少双鞋子？

(2)、若商场每天要盈利1750元,且让顾客尽可能多得实惠,每双鞋子应降价多少元？

查看试题解析
23. 小明在学习反比例函数后，为研究新函数 $y = \frac{1 + x}{x}$ ，先将函数变形为 $y = \frac{1}{x} + 1$ ，画图发现函数 $y = \frac{1 + x}{x}$ 的图象可以由函数 $y = \frac{1}{x}$ 的图象向上平移1个单位得到.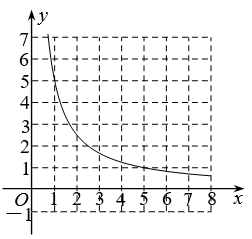

(1)、根据小明的发现，请你写出函数 $y = \frac{5 - x}{x}$ 的图象可以由反比例函数 $y = \frac{5}{x}$ 的图象经过怎样的平移得到；

(2)、在平面直角坐标系中，已知反比例函数 $y = \frac{5}{x}$ (x＞0)的图象如图所示，请在此坐标系中画出函数 $y = \frac{5 - x}{x}$ (x＞0)的图象；

(3)、若直线y=－x＋b与函数 $y = \frac{5 - x}{x}$ (x＞0)的图象没有交点，求b的取值范围.

查看试题解析
24. 如图，在菱形 $A B C D$ 中， $∠ D A B$ =60°， AB=2，点E是AB上的动点，作∠EDQ=60°交BC于点Q ，点P在AD上，PD=PE.

(1)、求证：AE=BQ；

(2)、连接PQ ， EQ ，当∠PEQ=90°时，求 $\frac{D E}{P Q}$ 的值；

(3)、当AE为何值时，△PEQ是等腰三角形.

查看试题解析