浙江省金华市东阳市2019届数学中考模拟试卷
试卷更新日期：2019-07-15 类型：中考模拟
一、选择题（共10小题,每题3分，共30分）
-
1. 若（ ）﹣5＝﹣3，则括号内的数是（ ）A、﹣2 B、﹣8 C、2 D、82. 以下由两个全等的30°直角三角板拼成的图形中，属于中心对称图形的是（ ）A、
B、
C、
D、
3. 如图所示零件的左视图是（ ）
A、
B、
C、
D、
4. 下列运算中，正确的是（ ）A、（﹣ ）﹣1＝﹣2 B、a3•a6＝a18 C、6a6÷3a2＝2a3 D、（﹣2ab2）2＝2a2b45. 如图，DE∥GF，A在DE上，C在GF上△ABC为等边三角形，其中∠EAC＝80°，则∠BCG度数为（ ）
A、20° B、10° C、25° D、30°6. 某校在“爱护地球，绿化祖国”的创建活动中，组织了100名学生开展植树造林活动，其植树情况整理如下表：植树棵树（单位：棵）
4
5
6
8
10
人数（人）
30
22
25
15
8
则这100名学生所植树棵树的中位数（ ）
A、22 B、5 C、5.5 D、67. 如图，在△ABC中，DE∥BC， ，DE＝4，则BC的长 （ ）
A、8 B、10 C、12 D、168. 将直线y=﹣x+a的图象向右平移2个单位后经过点A（3，3），则a的值为（ ）A、4 B、﹣4 C、2 D、﹣29. 如图，在矩形ABCD中，E是CD边的中点，且BE⊥AC于点F，连接DF，则下列结论错误的是 （ ）
A、△ADC∽△CFB B、AD＝DF C、 ＝ D、 ＝10. 如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y＝kx+12与⊙O交于B、C两点，则弦BC长的最小值 （ ）
A、24 B、10 C、8 D、25二、填空题（共6小题，每小题4分，共24分）
-
11. 分解因式：4m2﹣16n2＝ ．12. 不等式不等式3x≥x﹣5的最小整数解是.13. 如图，在边长为6的菱形ABCD中，分别以各顶点为圆心，以边长的一半为半径，在菱形内作四条圆弧，则图中阴影部分的周长是 ． （结果保留π）
14. 如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足S△PAB＝ S矩形ABCD，则点P到A、B两点距离之和PA+PB的最小值为.
15. 如图，点A是射线y═ （x≥0）上一点，过点A作AB⊥x轴于点B，以AB为边在其右侧作正方形ABCD，过点A的双曲线y＝ 交CD边于点E，则 的值为
16. 如图，把一个量角器与一块30°（∠CAB＝30°）角的三角板拼在一起，三角板的斜边AB与量角器所在圆的直径MN重合，现有射线CP绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB重合，就停止旋转。在旋转过程中，射线CP与量角器的半圆弧交于E．连接BE．
(1)、设旋转x秒后，点E处的读数为y，则y与x的函数关系式.(2)、当CP旋转.秒时，△BCE是等腰三角形。三、解答题（共8小题,66分）
-
17. 计算：﹣12016﹣（ ）﹣2+ ﹣cos60°18. 如图，已知矩形ABCD是一空旷场地上的小屋示意图，其中AB：AD＝2：1．拴住小狗的绳子一端固定在点A处，请根据下面条件分别画出小狗在小屋外最大活动区域．（小狗的大小不计）
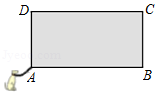
图1 图2(1)、若拴小狗的绳子长度与AD边长相等，在图1中画出小狗在屋外活动的最大区域；(2)、若拴小狗的绳子长度与AB边长相等，在图2中画出小狗在屋外活动的最大区域．19. 安装在屋顶的太阳能热水器的横截面示意图如图所示．已知集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O，⊙O的半径为0.2米，AO与屋面AB的夹角为32°，与铅垂线OD的夹角为40°，BF⊥AB，垂足为B，OD⊥AD，垂足为D，AB＝2米．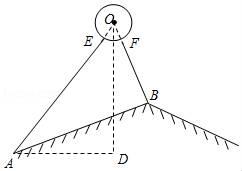
(1)、求支架BF的长；(2)、求屋面AB的坡度．（参考数据：tan18°≈ ，tan32°≈ ，tan40°≈ ）20. 如图，A是以BC为直径的⊙O上一点，过点B作⊙O的切线，与CA的延长线相交于点D，E是BD的中点，延长AE与CB的延长线相交于点F．
(1)、求证：AF是⊙O的切线；(2)、若BE＝5，BF＝12，求CD的长．21. 某销售公司年终进行业绩考核，人事部门把考核结果按照A，B，C，D四个等级，绘制成两个不完整的统计图，如图1，图2．
(1)、参加考试的人数是.扇形统计图中D部分所对应的圆心角的度数是.把条形统计图补充完整；(2)、公司领导计划从考核人员中选一人交流考核意见，求所选人员考核为A等级的概率；(3)、为推动公司进一步发展，公司决定计划两年内考核A等级的人数达到30人，求平均每年的增长率．（精确到0.01， ＝2.236）22. 有一科技小组进行了机器人行走性能试验．在试验场地有A、B、C三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A、B两点同时同向出发，经过7min同时到达C点，乙机器人始终以60m/min的速度行走，如图是甲、乙两机器人之间的距离y（m）与他们的行走时间x（min）之间的函数图象，请结合图象，回答下列问题：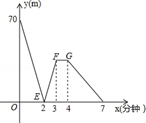
(1)、A、B两点之间的距离是.m，甲机器人前2min的速度为.m/min；(2)、若前3min甲机器人的速度不变，求线段EF所在直线的函数解析式；(3)、直接写出两机器人出发多长时间相距28m．23. 如图，已知点C（0，3），抛物线的顶点为A（2，0），与y轴交于点B（0，1），F在抛物线的对称轴上，且纵坐标为1．点P是抛物线上的一个动点，过点P作PM⊥x轴于点M，交直线CF于点H，设点P的横坐标为m．
(1)、求抛物线的解析式；(2)、若点P在直线CF下方的抛物线上，用含m的代数式表示线段PH的长，并求出线段PH的最大值及此时点P的坐标；(3)、当PF﹣PM＝1时，若将“使△PCF面积为2”的点P记作“巧点”，则存在多个“巧点”，请直接写出所有“巧点”的个数，并求出△PCF的周长最小的“巧点”的坐标．24. 如图，在平面直角坐标系中，A（0，4），B（3，4），P为线段OA上一动点，过O，P，B三点的圆交x轴正半轴于点C，连结AB，PC，BC，设OP＝m．
(1)、求证：当P与A重合时，四边形POCB是矩形．(2)、连结PB，求tan∠BPC的值．(3)、记该圆的圆心为M，连结OM，BM，当四边形POMB中有一组对边平行时，求所有满足条件的m的值．(4)、作点O关于PC的对称点O'，在点P的整个运动过程中，当点O'落在△APB的内部（含边界）时，请写出m的取值范围．