广西贵港市2019年中考数学试卷
试卷更新日期:2019-07-12 类型:中考真卷
一、选择题(本大题共12小题,每小题3分,共36分)
-
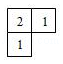
1. 计算(﹣1)3的结果是( )A、﹣1 B、1 C、﹣3 D、32. 某几何体的俯视图如图所示,图中数字表示该位置上的小正方体的个数,则这个几何体的主视图是( )
 A、
A、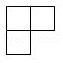 B、
B、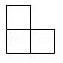 C、
C、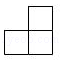 D、
D、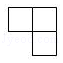 3. 若一组数据为:10,11,9,8,10,9,11,9,则这组数据的众数和中位数分别是( )A、9,9 B、10,9 C、9,9.5 D、11,104. 若分式 的值等于0,则x的值为( )A、±1 B、0 C、﹣1 D、15. 下列运算正确的是( )A、a3+(﹣a)3=﹣a6 B、(a+b)2=a2+b2 C、2a2•a=2a3 D、(ab2)3=a3b56. 若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n的值是( )A、1 B、3 C、5 D、77. 若α,β是关于x的一元二次方程x2﹣2x+m=0的两实根,且 =﹣ ,则m等于( )A、﹣2 B、﹣3 C、2 D、38. 下列命题中假命题是( )A、对顶角相等 B、直线y=x﹣5不经过第二象限 C、五边形的内角和为540° D、因式分解x3+x2+x=x(x2+x)9. 如图,AD是⊙O的直径, ,若∠AOB=40°,则圆周角∠BPC的度数是( )
3. 若一组数据为:10,11,9,8,10,9,11,9,则这组数据的众数和中位数分别是( )A、9,9 B、10,9 C、9,9.5 D、11,104. 若分式 的值等于0,则x的值为( )A、±1 B、0 C、﹣1 D、15. 下列运算正确的是( )A、a3+(﹣a)3=﹣a6 B、(a+b)2=a2+b2 C、2a2•a=2a3 D、(ab2)3=a3b56. 若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n的值是( )A、1 B、3 C、5 D、77. 若α,β是关于x的一元二次方程x2﹣2x+m=0的两实根,且 =﹣ ,则m等于( )A、﹣2 B、﹣3 C、2 D、38. 下列命题中假命题是( )A、对顶角相等 B、直线y=x﹣5不经过第二象限 C、五边形的内角和为540° D、因式分解x3+x2+x=x(x2+x)9. 如图,AD是⊙O的直径, ,若∠AOB=40°,则圆周角∠BPC的度数是( )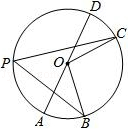 A、40° B、50° C、60° D、70°10. 将一条宽度为2cm的彩带按如图所示的方法折叠,折痕为AB,重叠部分为△ABC(图中阴影部分),若∠ACB=45°,则重叠部分的面积为( )
A、40° B、50° C、60° D、70°10. 将一条宽度为2cm的彩带按如图所示的方法折叠,折痕为AB,重叠部分为△ABC(图中阴影部分),若∠ACB=45°,则重叠部分的面积为( )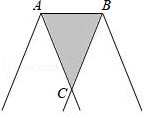 A、2 cm2 B、2 cm2 C、4cm2 D、4 cm211. 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为( )
A、2 cm2 B、2 cm2 C、4cm2 D、4 cm211. 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为( )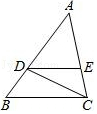 A、2 B、3 C、2 D、512. 如图,E是正方形ABCD的边AB的中点,点H与B关于CE对称,EH的延长线与AD交于点F,与CD的延长线交于点N,点P在AD的延长线上,作正方形DPMN,连接CP,记正方形ABCD,DPMN的面积分别为S1 , S2 , 则下列结论错误的是( )
A、2 B、3 C、2 D、512. 如图,E是正方形ABCD的边AB的中点,点H与B关于CE对称,EH的延长线与AD交于点F,与CD的延长线交于点N,点P在AD的延长线上,作正方形DPMN,连接CP,记正方形ABCD,DPMN的面积分别为S1 , S2 , 则下列结论错误的是( )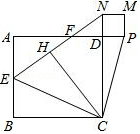 A、S1+S2=CP2 B、AF=2FD C、CD=4PD D、cos∠HCD=
A、S1+S2=CP2 B、AF=2FD C、CD=4PD D、cos∠HCD=二、填空题(本大题共6小题,每小题3分,共18分)
-
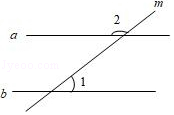
13. 有理数9的相反数是.14. 将实数3.18×10﹣5用小数表示为.15. 如图,直线a∥b,直线m与a,b均相交,若∠1=38°,则∠2=.
 16. 若随机掷一枚均匀的骰子,骰子的6个面上分别刻有1,2,3,4,5,6点,则点数不小于3的概率是.17. 如图,在扇形OAB中,半径OA与OB的夹角为120°,点A与点B的距离为2 ,若扇形OAB恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为.
16. 若随机掷一枚均匀的骰子,骰子的6个面上分别刻有1,2,3,4,5,6点,则点数不小于3的概率是.17. 如图,在扇形OAB中,半径OA与OB的夹角为120°,点A与点B的距离为2 ,若扇形OAB恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为.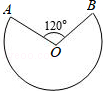 18. 我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2﹣4a>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=﹣1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是.
18. 我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2﹣4a>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=﹣1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是.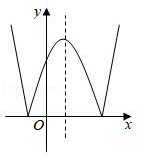
三、解答题(本大题共8小题,满分66分。)
-
19.(1)、计算: ﹣( ﹣3)0+( )﹣2﹣4sin30°;(2)、解不等式组: ,并在数轴上表示该不等式组的解集.20. 尺规作图(只保留作图痕迹,不要求写出作法):
如图,已知△ABC,请根据“SAS”基本事实作出△DEF,使△DEF≌△ABC.
 21. 如图,菱形ABCD的边AB在x轴上,点A的坐标为(1,0),点D(4,4)在反比例函数y= (x>0)的图象上,直线y= x+b经过点C,与y轴交于点E,连接AC,AE.
21. 如图,菱形ABCD的边AB在x轴上,点A的坐标为(1,0),点D(4,4)在反比例函数y= (x>0)的图象上,直线y= x+b经过点C,与y轴交于点E,连接AC,AE.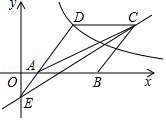 (1)、求k,b的值;(2)、求△ACE的面积.22. 为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩(x分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:
(1)、求k,b的值;(2)、求△ACE的面积.22. 为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩(x分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题: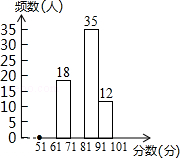
分数段(分)
频数(人)
频率
51≤x<61
a
0.1
61≤x<71
18
0.18
71≤x<81
b
n
81≤x<91
35
0.35
91≤x<101
12
0.12
合计
100
1
(1)、填空:a= , b= , n=;(2)、将频数分布直方图补充完整;(3)、该校对考试成绩为91≤x≤100的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数.23. 为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.(1)、求这两年藏书的年均增长率;(2)、经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?24. 如图,在矩形ABCD中,以BC边为直径作半圆O,OE⊥OA交CD边于点E,对角线AC与半圆O的另一个交点为P,连接AE.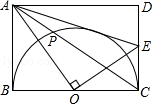 (1)、求证:AE是半圆O的切线;(2)、若PA=2,PC=4,求AE的长.25. 如图,已知抛物线y=ax2+bx+c的顶点为A(4,3),与y轴相交于点B(0,﹣5),对称轴为直线l,点M是线段AB的中点.
(1)、求证:AE是半圆O的切线;(2)、若PA=2,PC=4,求AE的长.25. 如图,已知抛物线y=ax2+bx+c的顶点为A(4,3),与y轴相交于点B(0,﹣5),对称轴为直线l,点M是线段AB的中点. (1)、求抛物线的表达式;(2)、写出点M的坐标并求直线AB的表达式;(3)、设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.26. 已知:△ABC是等腰直角三角形,∠BAC=90°,将△ABC绕点C顺时针方向旋转得到△A′B′C,记旋转角为α,当90°<α<180°时,作A′D⊥AC,垂足为D,A′D与B′C交于点E.
(1)、求抛物线的表达式;(2)、写出点M的坐标并求直线AB的表达式;(3)、设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.26. 已知:△ABC是等腰直角三角形,∠BAC=90°,将△ABC绕点C顺时针方向旋转得到△A′B′C,记旋转角为α,当90°<α<180°时,作A′D⊥AC,垂足为D,A′D与B′C交于点E.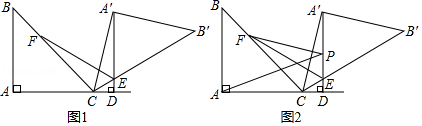 (1)、如图1,当∠CA′D=15°时,作∠A′EC的平分线EF交BC于点F.
(1)、如图1,当∠CA′D=15°时,作∠A′EC的平分线EF交BC于点F.①写出旋转角α的度数;
②求证:EA′+EC=EF;
(2)、如图2,在(1)的条件下,设P是直线A′D上的一个动点,连接PA,PF,若AB= ,求线段PA+PF的最小值.(结果保留根号)