海南省2019年中考数学试卷
试卷更新日期:2019-07-12 类型:中考真卷
一、单选题
-
1. 如果收入100元记作+100元,那么支出100元记作( )A、-100元 B、+100元 C、-200元 D、+200元2. 当m=-1时,代数式2m+3的值是( )A、-1 B、0 C、1 D、23. 下列运算正确的是( )A、 B、 C、 D、4. 分式方程 的解是( )A、x=1 B、x=-1 C、x=2 D、x=-25. 海口市首条越江隧道﹣﹣文明东越江通道项目将于2020年4月份完工,该项目总投资3710000000元.数据3710000000用科学记数法表示为( )A、 B、 C、 D、6. 如图是由5个大小相同的小正方体摆成的几何体,它的俯视图是( )
 A、
A、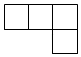 B、
B、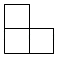 C、
C、 D、
D、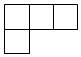 7. 如果反比例函数 (a是常数)的图象在第一、三象限,那么a的取值范围是( )A、a<0 B、a>0 C、a<2 D、a>28. 如图,在平面直角坐标系中,已知点 ,点 ,平移线段AB,使点A落在点 处,则点B的对应点 的坐标为( )
7. 如果反比例函数 (a是常数)的图象在第一、三象限,那么a的取值范围是( )A、a<0 B、a>0 C、a<2 D、a>28. 如图,在平面直角坐标系中,已知点 ,点 ,平移线段AB,使点A落在点 处,则点B的对应点 的坐标为( )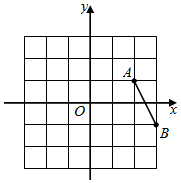 A、 B、 C、 D、9. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )
A、 B、 C、 D、9. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )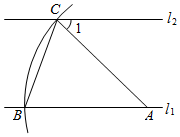 A、 B、 C、 D、10. 某路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小明到达该路口时,遇到绿灯的概率是( )A、 B、 C、 D、11. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )
A、 B、 C、 D、10. 某路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小明到达该路口时,遇到绿灯的概率是( )A、 B、 C、 D、11. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )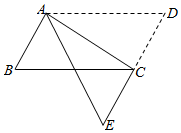 A、12 B、15 C、18 D、2112. 如图,在 中, , , .点P是边AC上一动点,过点P作 交BC于点Q,D为线段PQ的中点,当BD平分 时,AP的长度为( )
A、12 B、15 C、18 D、2112. 如图,在 中, , , .点P是边AC上一动点,过点P作 交BC于点Q,D为线段PQ的中点,当BD平分 时,AP的长度为( )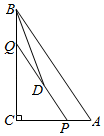 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 因式分解: .14. 如图, 与正五边形ABCDE的边AB、DE分别相切于点B、D,则劣弧 所对的圆心角 的大小为度.
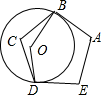 15. 如图,将 的斜边AB绕点A顺时针旋转 得到AE,直角边AC绕点A逆时针旋转 得到AF,连结EF.若 , ,且 ,则 .
15. 如图,将 的斜边AB绕点A顺时针旋转 得到AE,直角边AC绕点A逆时针旋转 得到AF,连结EF.若 , ,且 ,则 . 16. 有2019个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是0,第二个数是1,那么前6个数的和是 , 这2019个数的和是.
16. 有2019个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是0,第二个数是1,那么前6个数的和是 , 这2019个数的和是.三、解答题
-
17.(1)、计算: ;(2)、解不等式组 ,并求出它的整数解.18. 时下正是海南百香果丰收的季节,张阿姨到“海南爱心扶贫网”上选购百香果,若购买2千克“红土”百香果和1千克“黄金”百香果需付80元,若购买1千克“红土”百香果和3千克“黄金”百香果需付115元.请问这两种百香果每千克各是多少元?19. 为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
表1 知识竞赛成绩分组统计表
组别
分数/分
频数
A
a
B
10
C
14
D
18
 (1)、本次调查一共随机抽取了个参赛学生的成绩;(2)、表1中 ;(3)、所抽取的参赛学生的成绩的中位数落在的“组别”是;(4)、请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有人.20. 如图是某区域的平面示意图,码头A在观测站B的正东方向,码头A的北偏西 方向上有一小岛C,小岛C在观测站B的北偏西 方向上,码头A到小岛C的距离AC为10海里.
(1)、本次调查一共随机抽取了个参赛学生的成绩;(2)、表1中 ;(3)、所抽取的参赛学生的成绩的中位数落在的“组别”是;(4)、请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有人.20. 如图是某区域的平面示意图,码头A在观测站B的正东方向,码头A的北偏西 方向上有一小岛C,小岛C在观测站B的北偏西 方向上,码头A到小岛C的距离AC为10海里.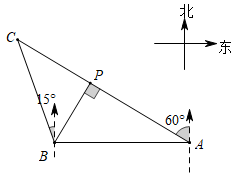 (1)、填空: 度, 度;(2)、求观测站B到AC的距离BP(结果保留根号).21. 如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)、填空: 度, 度;(2)、求观测站B到AC的距离BP(结果保留根号).21. 如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.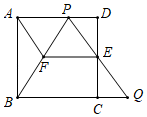 (1)、求证: ;(2)、过点E作 交PB于点F,连结AF,当 时,①求证:四边形AFEP是平行四边形;
(1)、求证: ;(2)、过点E作 交PB于点F,连结AF,当 时,①求证:四边形AFEP是平行四边形;②请判断四边形AFEP是否为菱形,并说明理由.
22. 如图,已知抛物线 经过 , 两点,与x轴的另一个交点为C,顶点为D,连结CD.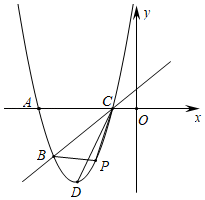 (1)、求该抛物线的表达式;(2)、点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
(1)、求该抛物线的表达式;(2)、点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.①当点P在直线BC的下方运动时,求 的面积的最大值;
②该抛物线上是否存在点P,使得 若存在,求出所有点P的坐标;若不存在,请说明理由.