2019年浙江省中考数学分类汇编专题07:图形(三角形)
试卷更新日期:2019-07-11 类型:二轮复习
一、单选题
-
1. 下列长度的三条线段,能组成三角形的是( )A、3,4,8 B、5,6,10 C、5,5,11 D、5,6,112. 已知直线m∥n,将一块含45°角的直角三角板ABC按如图方式放置,其中斜边BC与直线n交于点D.若∠1=25°,则∠2的度数为( )
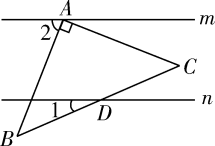 A、60° B、65° C、70° D、75°3. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、84. 如图,墙上钉着三根木条,a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是( )
A、60° B、65° C、70° D、75°3. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、84. 如图,墙上钉着三根木条,a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是( )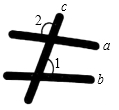 A、5° B、10° C、30° D、70°5. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A、5° B、10° C、30° D、70°5. 如图,已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )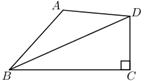 A、24 B、30 C、36 D、426. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=75°,则∠CDE的度数是( )
A、24 B、30 C、36 D、426. “三等分角”大约是在公元前五世纪由古希腊人提出来的。借助如图所示的“三等分角仪”能三等分任一角。这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=75°,则∠CDE的度数是( )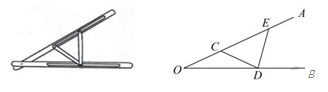 A、60° B、65° C、75° D、80°7. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形。则原来的纸带宽为( )
A、60° B、65° C、75° D、80°7. 如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形。则原来的纸带宽为( )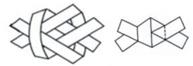 A、1 B、 C、 D、28. 在△ABC中,若一个内角等于另两个内角的差,则( )A、必有一个内角等于30° B、必有一个内角等于45° C、必有一个内角等于60° D、必有一个内角等于90°9. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A、1 B、 C、 D、28. 在△ABC中,若一个内角等于另两个内角的差,则( )A、必有一个内角等于30° B、必有一个内角等于45° C、必有一个内角等于60° D、必有一个内角等于90°9. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
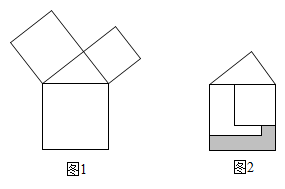 A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和10. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和10. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )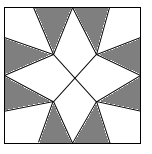 A、 :1 B、3:2 C、 :1 D、 :2
A、 :1 B、3:2 C、 :1 D、 :2二、填空题
-
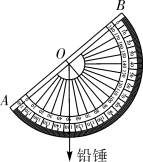
11. 如图,在量角器的圆心O处下挂一铅锤,制作了一个简易测倾仪。量角器的O刻度线AB对准楼顶时,铅垂线对应的读数是50°,则此时观察楼顶的仰角度数是 .
三、作图题
-
12. 如图,在7×6的方格中,△ABC的顶点均在格点上,试按要求画出线段EF(E,F均为格点),各画出一条即可。
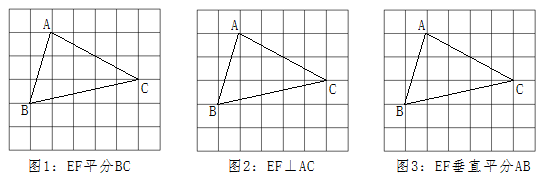 13. 如图,在7×5的方格纸ABCD中,请按要求画图,且所画格点三角形与格点四边形的顶点均不与点A,B,C,D重合.
13. 如图,在7×5的方格纸ABCD中,请按要求画图,且所画格点三角形与格点四边形的顶点均不与点A,B,C,D重合.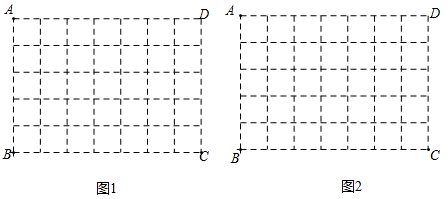 (1)、在图1中画一个格点△EFG,使点E,F,G分别落在边AB,BC,CD上,且∠EFG=90°;(2)、在图2中画一个格点四边形MNPQ,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且MP=NQ.14. 定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)、在图1中画一个格点△EFG,使点E,F,G分别落在边AB,BC,CD上,且∠EFG=90°;(2)、在图2中画一个格点四边形MNPQ,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且MP=NQ.14. 定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线. (1)、如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.
(1)、如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点.求证:四边形ABEF是邻余四边形。
(2)、如图2,在5×4的方格纸中,A,B在格点上,请画出一个符合条件的邻余四边形ABEF,使AB是邻余线,E,F在格点上,(3)、如图3,在(1)的条件下,取EF中点M,连结DM并延长交AB于点Q,延长EF交AC于点N.若N为AC的中点,DE=2BE,QB=3,求邻余线AB的长。四、综合题
-
15. 如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
 (1)、求证:△BDE≌△CDF;(2)、当AD⊥BC,AE=1,CF=2时,求AC的长.16. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
(1)、求证:△BDE≌△CDF;(2)、当AD⊥BC,AE=1,CF=2时,求AC的长.16. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.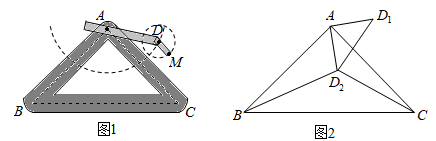 (1)、在旋转过程中,
(1)、在旋转过程中,①当A,D,M三点在同一直线上时,求AM的长。
②当A,D,M三点为同一直角三角形的顶点时,求AM的长。
(2)、若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2 , 如图2.此时∠AD2C=135°,CD2=60,求BD2的长.17. 如图,在△ABC中,AC<AB<BC.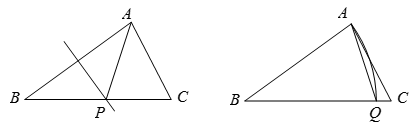 (1)、已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.(2)、以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q.连接AQ若∠AQC=3∠B,求∠B的度数.18. 我们知道,各个角都相等,各条边都相等的多边形叫做正多边形,对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形
(1)、已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.(2)、以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q.连接AQ若∠AQC=3∠B,求∠B的度数.18. 我们知道,各个角都相等,各条边都相等的多边形叫做正多边形,对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形 (1)、已知凸五边形ABCDE的各条边都相等
(1)、已知凸五边形ABCDE的各条边都相等①如图1,若AC=AD=BE=BD=CE,求证:五边形ABCDE是正五边形
②2如图2,若AC=BE=CE,请判断五边形ABCDE是不是正五边形,并说明理由
(2)、判断下列命题的真假,(在括号内填写“真”或“假”),如图3,已知凸六边形ABCDEF的各条边都相等①若AC=CE=EA,则六边形ABCDEF是正六边形()
②若AD=BE=CF,则六边形ABCDEF是正六边形()
-