2019年浙江省中考数学分类汇编专题08:图形(四边形)
试卷更新日期:2019-07-11 类型:二轮复习
一、单选题
-
1. 正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( )
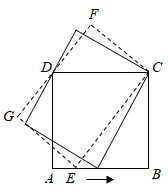 A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变
A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变二、填空题
-
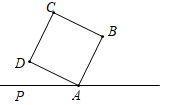
2. 如图,在直线AP上方有一个正方形ABCD,∠PAD=30°,以点B为圆心,AB长为半径作弧点A,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连结ED,则∠ADE的度数为 。
 3. 把边长为2的正方形纸片ABCD分割成如图四块,其中点O为正方形的中心,点E,F分别为AB,AD的中点,用这四块纸片拼成与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠无缝隙),则四边形MNPQ的周长是。
3. 把边长为2的正方形纸片ABCD分割成如图四块,其中点O为正方形的中心,点E,F分别为AB,AD的中点,用这四块纸片拼成与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠无缝隙),则四边形MNPQ的周长是。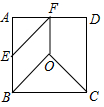 4. 七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”. 由边长为4√2的正方形ABCD可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型(其中点Q、R分别与图2中的点E、G重合,点P在边EH上),则“拼搏兔”所在正方形EFGH的边长是.
4. 七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”. 由边长为4√2的正方形ABCD可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型(其中点Q、R分别与图2中的点E、G重合,点P在边EH上),则“拼搏兔”所在正方形EFGH的边长是.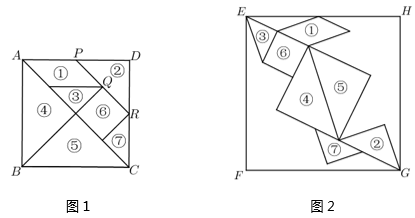
三、作图题
-
5. 如图,在4×4的方格子中,△ABC的三个顶点都在格点上,
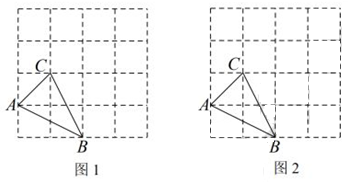 (1)、在图1中画出线段CD,使CD⊥CB,其中D是格点,(2)、在图2中画出平行四边形ABEC,其中E是格点.
(1)、在图1中画出线段CD,使CD⊥CB,其中D是格点,(2)、在图2中画出平行四边形ABEC,其中E是格点.四、解答题
-
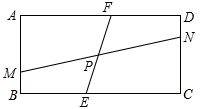
6. 如图,在矩形 ABCD中,点 E,F 在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明.
 7. 已知:如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF.求证:AE=AF.
7. 已知:如图,在菱形ABCD中,点E,F分别在边BC,CD上,且BE=DF,连结AE,AF.求证:AE=AF.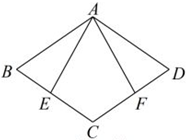 8. 如图,已知在△ABC中,D,E,F分别是AB,BC,AC的中点,连结DF,EF,BF.
8. 如图,已知在△ABC中,D,E,F分别是AB,BC,AC的中点,连结DF,EF,BF. (1)、求证:四边形BEFD是平行四边形;(2)、若∠AFB=90°,AB=6,求四边形BEFD的周长.9. 如图,已知正方形ABCD的边长为1,正方形CEFG的面积为S1 , 点E在DC边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为 S2 , 且S1=S2.
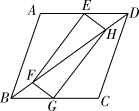
(1)、求证:四边形BEFD是平行四边形;(2)、若∠AFB=90°,AB=6,求四边形BEFD的周长.9. 如图,已知正方形ABCD的边长为1,正方形CEFG的面积为S1 , 点E在DC边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为 S2 , 且S1=S2. (1)、求线段CE的长.(2)、若点日为BC边的中点,连接HD,求证:HD=HG.
(1)、求线段CE的长.(2)、若点日为BC边的中点,连接HD,求证:HD=HG.
-
-