2019年浙江省中考数学分类汇编专题09：图形（圆）
试卷更新日期：2019-07-11 类型：二轮复习
一、单选题
-
1. 若扇形的圆心角为90°，半径为6，则该扇形的弧长为（ ）A、 B、 C、 D、2. 如图，已知⊙O上三点A，B，C，半径OC=1，∠ABC=30°，切线PA交OC延长线于点P，则PA的长为（ ）
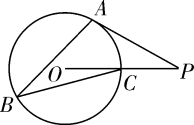A、2 B、 C、 D、3. 如图，△ABC内接于⊙O，∠B=65°，∠C=70°，若BC=2 ，则 的长为（ ）
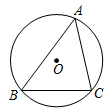A、π B、 π C、2π D、 π4. 如图，等边三角形ABC的边长为8，以BC上一点O为圆心的圆分别与边AB，AC相切，则⊙O的半径为（ ）
A、2 B、3 C、4 D、4-5. 已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积是（ ）A、60πcm2 B、65πcm2 C、120πcm2 D、130πcm26. 如图，已知正五边形 ABCDE内接于⊙O，连结BD，则∠ABD的度数是（ ）
A、60° B、70° C、72° D、144°7. 一块圆形宣传标志牌如图所示，点A，B，C在⊙O上，CD垂直平分AB于点D，现测得AB=8dm，DC=2dm，则圆形标志牌的半径为（ ）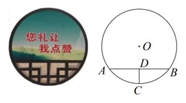
A、6dm B、5dm C、4dm D、3dm8. 如图，P为⊙O外一点，PA，PB分别切⊙O于A，B两点，若PA=3，则PB=（ ）
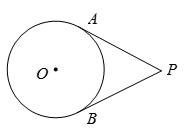A、2 B、3 C、4 D、59. 如图所示，矩形纸片ABCD中，AD=6cm，把它分割成正方形纸片ABFE和矩形纸片EFCD后，分别裁出扇形ABF和半径最大的圆，恰好能作为一个圆锥的侧面和底面，则AB的长为（ ）
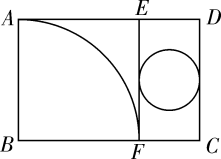A、3.5cm B、4cm C、4.5cm D、5cm10. 如图物体由两个圆锥组成，其主视图中，∠A=90°，∠ABC=105°，若上面圆锥的侧面积为1，则下面圆锥的侧面积为（ ）
A、2 B、 C、 D、二、填空题
-
11. 如图，⊙O分别切∠BAC的两边AB，AC于点E，F，点P在优弧 上．若∠BAC＝66°，则∠EPF等于度．
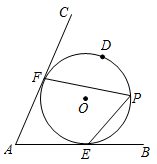12. 如图，在⊙O中，弦 ，点C在AB上移动，连结OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为 ．
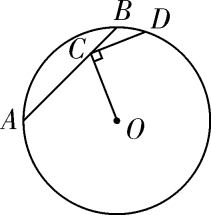13. 如图，AC是圆内接四边形ABCD的一条对角线，点D关于AC的对称点E在边BC上连接AE.若∠ABC=64°，则∠BAE的度数为.
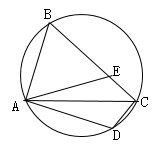14. 已知一条弧所对的圆周角的度数是15°，则它所对的圆心角的度数是.15. 如图是一个圆锥形冰淇淋外壳（不计厚度）.已知其母线长为12cm，底面圆半径为3cm，则这个冰淇淋外壳的侧面积等于cm2（结果精确到个位）.
16. 如图，Rt△ABC中，∠C=90°，AC=12，点D在边BC上，CD=5，BD=13.点P是线段AD上一动点，当半径为6的OP与△ABC的一边相切时，AP的长为.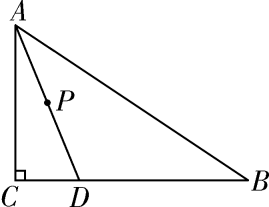
三、综合题
-
17. 在屏幕上有如下内容：
如图，△ABC内接于⊙O，直径AB的长为2，过点C的切线交AB的题长线于点D.张老师要求添加条件后，编制一道题目，并解答。
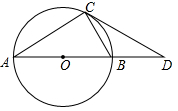(1)、在屏幕内容中添加条件∠D=30°，求AD的长，请你解答。(2)、以下是小明、小思的对话：小明：我加的条件是BD=1，就可以求出AD的长。
小聪：你这样太简单了，我加的是∠A=30°，连结OC，就可证明△ACB与△DCO全等。
参考此对话：在屏幕内容中添加条件，编制一道题（可以添线、添字母），并解答。
18. 如图，在等腰△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为E.
(1)、求证：DE是⊙O的切线.(2)、若DE= ，∠C=30°，求 的长。19. 如图，在△ABC中，∠BAC＝90°，点E在BC边上，且CA＝CE，过A，C，E三点的⊙O交AB于另一点F，作直径AD，连结DE并延长交AB于点G，连结CD，CF．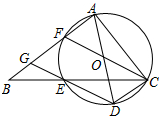
(1)、求证：四边形DCFG是平行四边形；(2)、当BE＝4，CD＝ AB时，求⊙O的直径长．20. 已知在平面直角坐标系xOy中，直线l1分别交x轴和y轴于点A(-3，0)，B(0，3).
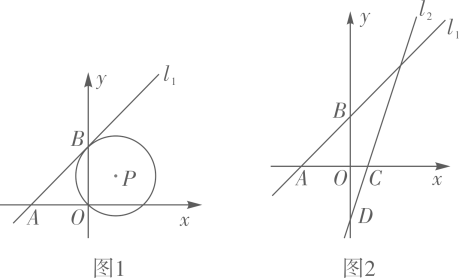(1)、如图1，已知⊙P经过点O，且与直线l1相切于点B，求⊙P的直径长；(2)、如图2，已知直线l2： y＝3x-3分别交x轴和y轴于点C和点D，点Q是直线l2上的一个动点，以Q为圆心， 为半径画圆.①当点Q与点C重合时，求证： 直线l1与⊙Q相切；
②设⊙Q与直线l1相交于M，N两点， 连结QM，QN. 问：是否存在这样的点Q，使得△QMN是等腰直角三角形，若存在，求出点Q的坐标；若不存在，请说明理由.
21. 如图，在Rt△ABC中，∠C=90°，AC=6，∠BAC=60°，AD平分∠BAC交BC于点D，过点D作DE∥AC交AB于点E，点M是线段AD上的动点，连结BM并延长分别交DE，AC于点F、G。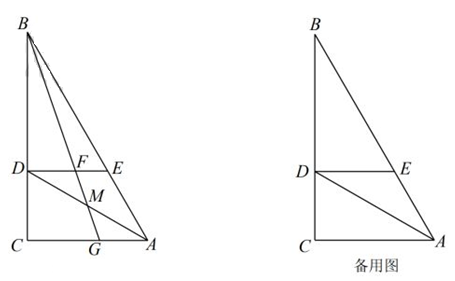
(1)、求CD的长。(2)、若点M是线段AD的中点，求 的值。(3)、请问当DM的长满足什么条件时，在线段DE上恰好只有一点P，使得∠CPG=60°?22. 如图，已知锐角三角形ABC内接于⊙O，OD⊥BC于点D，连接OA.
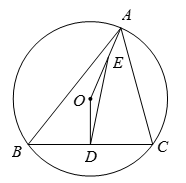(1)、若∠BAC=60°，①求证：OD= OA.
②当OA=1时，求△ABC面积的最大值。
(2)、点E在线段OA上，（OE=OD.连接DE，设∠ABC=m∠OED.∠ACB=n∠OED（m，n是正数）.若∠ABC<∠ACB，求证：m-n+2=0.
23. 如图1， O经过等边△ABC的顶点A，C（圆心O在△ABC内），分别与AB，CB的延长线交于点D，E，连结DE，BF⊥EC交AE于点F.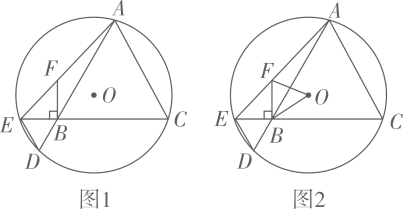
(1)、求证：BD=BE.(2)、当AF：EF=3：2，AC=6时，求AE的长。(3)、设 =x，tan∠DAE=y.①求y关于x的函数表达式；
②如图2，连结OF，OB，若△AEC的面积是△OFB面积的10倍，求y的值