2019年浙江省中考数学分类汇编专题11：锐角三角函数

试卷更新日期：2019-07-11 类型：二轮复习

进入出卷网下载

一、单选题

1. 某简易房示意图如图所示，它是一个轴对称图形，则坡屋顶上弦杆AB的长为（）

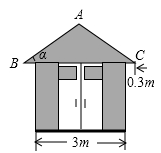A、 $\frac{9}{5 \sin α}$ 米 B、 $\frac{9}{5 \cos α}$ 米 C、 $\frac{5}{9 \sin α}$ 米 D、 $\frac{5}{9 \cos α}$ 米

查看试题解析
2. 如图1长、宽均为3，高为8的长方体容器，放置在水平桌面上，里面盛有水，水面高为6，绕底面一楼进行旋转倾斜后，水面恰好触到容器口边缘，图2是此时的示意图，则图2中水面高度为（）

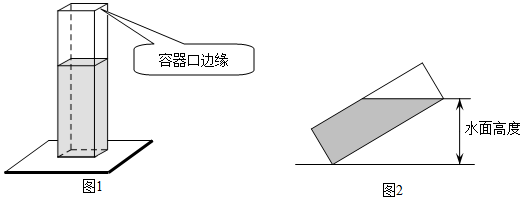A、 $\frac{24}{5}$ B、 $\frac{32}{5}$ C、 $\frac{12 \sqrt{34}}{17}$ D、 $\frac{20 \sqrt{34}}{17}$

查看试题解析
3. 如图，矩形ABCD的对角线交于点O，已知AB=m，∠BAC=∠α，则下列结论错误的是（）

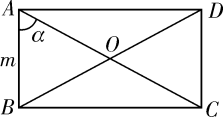A、∠BDC=∠α B、BC=m·tanα C、AO= $\frac{m}{2 \sin a}$ D、BD= $\frac{m}{\cos a}$

查看试题解析
4. 如图，有两张矩形纸片ABCD和EFGH、AB=EF=2cm，BC=FG=8cm，把纸片ABCD交叉叠放在纸片EFGH上，使重叠部分为平行四边形，且点D与点G重合，当两张纸片交叉所成的角最小α时，tanα等于（）

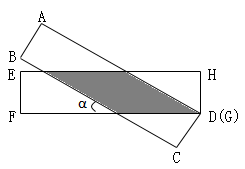A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{8}{17}$ D、 $\frac{8}{15}$

查看试题解析
5. 如图，一块矩形木板ABCD斜靠在墙边（OC⊥OB，点A，B，C，D，O在同一平面内）.已知AB=a，AD=b，∠BCO=x，则点A到OC的距离等于（）

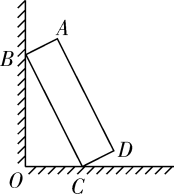A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx

查看试题解析

二、填空题

6. 如图，在△ABC中，若∠A=45°，AC^2-BC²= $\frac{\sqrt{5}}{5}$ AB² ，则tanC=。

查看试题解析
7. 如图，一副含30°和45°角的三角板 $A B C$ 和 $E D F$ 拼合在个平面上，边 $A C$ 与 $E F$ 重合， $A C = 12 c m$ ．当点 $E$ 从点 $A$ 出发沿 $A C$ 方向滑动时，点 $F$ 同时从点 $C$ 出发沿射线 $B C$ 方向滑动．当点 $E$ 从点 $A$ 滑动到点 $C$ 时，点 $D$ 运动的路径长为 $c m$ ；连接 $B D$ ，则△ $A B D$ 的面积最大值为 $c m^{2}$ ．

查看试题解析
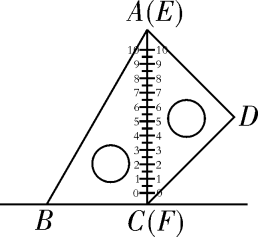8. 有一种落地晾衣架如图1所示，其原理是通过改变两根支撑杆夹角的度数来调整晾衣杆的高度. 图2是支撑杆的平面示意图，AB和CD分别是两根不同长度的支撑杆，夹角∠BOD＝α. 若AO＝85cm，BO＝DO＝65cm. 问：当α＝74°，较长支撑杆的端点A离地面的高度h约为cm.（参考数据： sin37≈0.6，cos3≈0.8，sin53≈0.8，cos53≈0.6.）

查看试题解析
9. 如图，人字梯AB，AC的长都为2米。当a=50°时，人字梯顶端高地面的高度AD是米（结果精确到0.1m。参考依据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）

查看试题解析
10. 在直角三角形ABC中，若2AB=AC，则cosC=.

查看试题解析
11. 如图，某海防响所O发现在它的西北方向，距离哨所400米的A处有一般船向正东方向航行，航行一段时间后到达哨所北偏东60°方向的B处，则此时这般船与哨所的距离OB约为米。（精确到1米，参考数据： $\sqrt{2}$ =1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
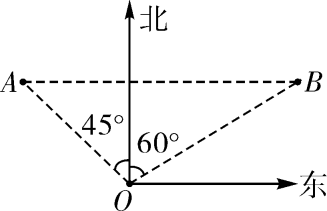12. 图2、图3是某公共汽车双开门的俯视示意图，ME，EF，FN是门轴的滑动轨道，∠E=∠F=90°，两门AB，CD的门轴A，B，C，D都在滑动轨道上．两门关闭时（图2），A，D分别在E，F处，门缝忽略不计（即B，C重合）；两门同时开启，A，D分别沿E→M，F→N的方向匀速滑动，带动B，C滑动；B到达E时，C恰好到达F，此时两门完全开启。已知AB=50cm，CD=40cm．

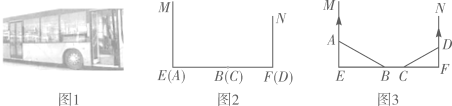(1)、如图3，当∠ABE=30°时，BC= cm．

(2)、在（1）的基础上，当A向M方向继续滑动15cm时，四边形ABCD的面积为cm² ．

查看试题解析

三、解答题

13. 某挖掘机的底座高 $A B = 0.8$ 米，动臂 $B C = 1.2$ 米， $C D = 1.5$ 米， $B C$ 与 $C D$ 的固定夹角∠ $B C D$ =140°．初始位置如图1，斗杆顶点 $D$ 与铲斗顶点 $E$ 所在直线 $D E$ 垂直地面 $A M$ 于点 $E$ ，测得∠ $C D E$ =70°(示意图2)．工作时如图3，动臂 $B C$ 会绕点 $B$ 转动，当点 $A$ ， $B$ ， $C$ 在同一直线时，斗杆顶点 $D$ 升至最高点(示意图4)．

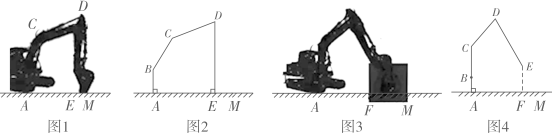
（考数据： $\sin 50^{\circ} \approx 0.77$ ， $\cos 50^{\circ} \approx 0.64$ ， $\sin 70^{\circ} \approx 0.94$ ， $\cos 70^{\circ} \approx 0.34$ ， $\sqrt{3 \approx} 1.73$ ）

(1)、求挖掘机在初始位置时动臂 $B C$ 与 $A B$ 的夹角∠ $A B C$ 的度数．

(2)、问斗杆顶点 $D$ 的最高点比初始位置高了多少米(精确到0.1米)?

查看试题解析
14. 如图1为放置在水平桌面l上的台灯，底座的高AB为5cm，长度均为20cm的连杆BC，CD与AB始终在同一平面上。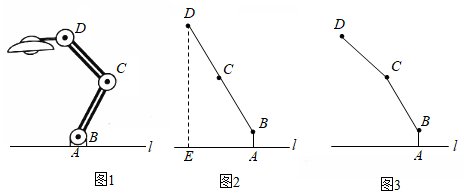

(1)、转动连杆BC，CD，使∠BCD成平角，∠ABC=150°，如图2，求连杆端点D离桌面l的高度DE.

(2)、将（1）中的连杆CD再绕点C逆时针旋转，使∠BCD=165°，如图3，问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少？（精确到0.1cm，参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
15. 图1是一辆在平地上滑行的滑板车，图2是其示意图，已知车杆AB长92cm，车杆与脚踏板所成的角∠ABC=70°，前后轮子的半径均为6cm，求把手A离地面的高度（结果保留小数点后一位：参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

查看试题解析
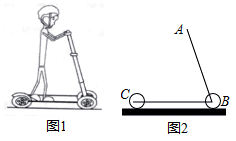16. 如图1，已知在平面直角坐标系xOy中，四边形OABC是矩形点A，C分别在x轴和y轴的正半轴上，连结AC，OA＝3，tan∠OAC＝ $\frac{\sqrt{3}}{3}$ ，D是BC的中点.

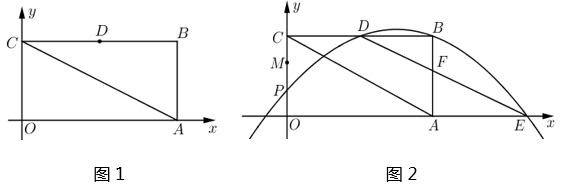(1)、求OC的长和点D的坐标；

(2)、如图2，M是线段OC上的点，OM＝ $\frac{2}{3}$ OC，点P是线段OM上的一个动点，经过P，D，B三点的抛物线交x轴的正半轴于点E，连结DE交AB于点F
①将△DBF沿DE所在的直线翻折，若点B恰好落在AC上，求此时BF的长和点E的坐标；

②以线段DF为边，在DF所在直线的右上方作等边△DFG，当动点P从点O运动到点M时，点G也随之运动，请直接写出点G运动路径的长.

查看试题解析