2019年浙江省中考数学分类汇编专题06:函数及其图象(二次函数)
试卷更新日期:2019-07-11 类型:二轮复习
一、单选题
-
1. 二次函数y=(x-1)2+3图象的顶点坐标是( )A、(1,3) B、(1,-3) C、(-1,3) D、(-1,-3)2. 已知二次函数 ,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )A、有最大值﹣1,有最小值﹣2 B、有最大值0,有最小值﹣1 C、有最大值7,有最小值﹣1 D、有最大值7,有最小值﹣23. 小飞研究二次函数 ( 为常数)性质时如下结论:
①这个函数图象的顶点始终在直线 上;②存在一个 的值,使得函数图象的顶点与 轴的两个交点构成等腰直角三角形;③点 与点 在函数图象上,若 , ,则 ;④当 时, 随 的增大而增大,则 的取值范围为 其中错误结论的序号是( )
A、① B、② C、③ D、④4. D在平面直角坐标系中,抛物线y=(x+5)(x-3)经变换后得到抛物线y=(x+3)(x-5),则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移8个单位 D、向右平移8个单位5. 已知a,b是非零实数, ,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是( )A、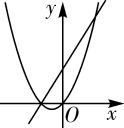 B、
B、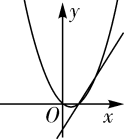 C、
C、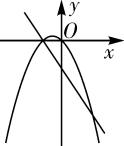 D、
D、 6. 在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则( )A、M=N-1或M=N+1 B、M=N-1或M=N+2 C、M=N或M=N+1 D、M=N或M=N-1
6. 在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则( )A、M=N-1或M=N+1 B、M=N-1或M=N+2 C、M=N或M=N+1 D、M=N或M=N-1二、作图题
-
7. 某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数y(间)与每间标准房的价格x(元)的数据如下表:
x(元)
…
190
200
210
220
…
y(间)
…
65
60
55
50
…
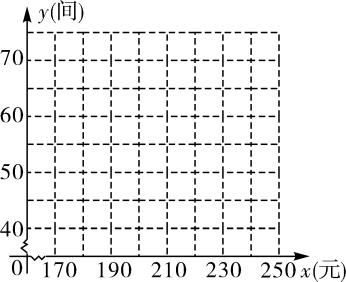 (1)、根据所给数据在坐标系中描出相应的点,并画出图象。(2)、求y关于x的函数表达式、并写出自变量x的取值范围.(3)、设客房的日营业额为w(元)。若不考虑其他因素,问宾馆标准房的价格定为多少元时。客房的日营业额最大?最大为多少元?
(1)、根据所给数据在坐标系中描出相应的点,并画出图象。(2)、求y关于x的函数表达式、并写出自变量x的取值范围.(3)、设客房的日营业额为w(元)。若不考虑其他因素,问宾馆标准房的价格定为多少元时。客房的日营业额最大?最大为多少元?三、综合题
-
8. 如图,在平面直角坐标系中,二次函数 的图象交x轴于点A,B(点A在点B的左侧).
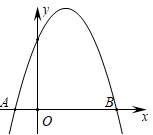 (1)、求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;(2)、把点B向上平移m个单位得点B1 . 若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m , n的值.9. 某农作物的生长率 与温度 ( )有如下关系:如图,当10≤ ≤25 时可近似用函数 刻画;
(1)、求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;(2)、把点B向上平移m个单位得点B1 . 若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m , n的值.9. 某农作物的生长率 与温度 ( )有如下关系:如图,当10≤ ≤25 时可近似用函数 刻画;当25≤ ≤37 时可近似用函数 刻画.
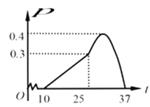 (1)、求 的值.(2)、按照经验,该作物提前上市的天数 (天)与生长率 满足函数关系,部分数据如下:
(1)、求 的值.(2)、按照经验,该作物提前上市的天数 (天)与生长率 满足函数关系,部分数据如下:生长率
0.2
0.25
0.3
0.35
提前上市的天数 (天)
0
5
10
15
求:①求 关于 的函数表达式;
②请用含 的代数式表示
③天气寒冷,大棚加温可改变农作物生长速度.在大棚恒温20℃时每天的成本为100元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到20≤t≤25时的成本为200元/天,但若加温到25<t≤37,由于要采用特殊方法,成本增加到400元/天,问加温到多少度时增加的利润最大?并说明理由。(注:农作物上市售出后大鹏暂停使用)
10. 某农作物的生长率 与温度 ( )有如下关系:如图1,当10≤ ≤25 时可近似用函数 刻画;当25≤ ≤37 时可近似用函数 刻画.
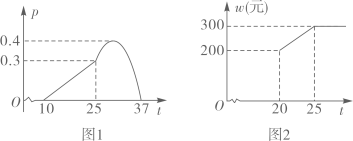 (1)、求 的值.(2)、按照经验,该作物提前上市的天数 (天)与生长率 满足函数关系:
(1)、求 的值.(2)、按照经验,该作物提前上市的天数 (天)与生长率 满足函数关系:生长率
0.2
0.25
0.3
0.35
提前上市的天数 (天)
0
5
10
15
①请运用已学的知识,求 关于 的函数表达式;
②请用含 的代数式表示
(3)、天气寒冷,大棚加温可改变农作物生长速度.在(2)的条件下,原计划大棚恒温20℃时,每天的成本为200元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此给大棚继续加温,加温后每天成本 (元)与大棚温度 ( )之间的关系如图2.问提前上市多少天时增加的利润最大?并求这个最大利润(农作物上市售出后大棚暂停使用).11. 已知抛物线y=2x2-4x+c与x轴有两个不同的交点.(1)、求c的取值范围;(2)、若抛物线y=2x2-4x+c经过点A(2,m)和点B(3,n),试比较m与n的大小,并说明理由.12. 如图,已知二次函数y=x2+ax+3的图象经过点P(-2,3).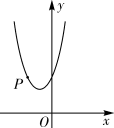 (1)、求a的值和图象的顶点坐标。(2)、点Q(m,n)在该二次函数图象上.
(1)、求a的值和图象的顶点坐标。(2)、点Q(m,n)在该二次函数图象上.①当m=2时,求n的值;
②若点Q到y轴的距离小于2,请根据图象直接写出n的取值范围.
13. 有一块形状如图的五边形余料ABCDE,AB=AE=6,BC=5,∠A=∠B=90°, ∠C=135°. ∠E>90°.要在这块余料中截取一块矩形材料,其中一条边在AE上,并使所截矩形材料的面积尽可能大。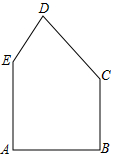 (1)、若所截矩形材料的一条边是BC或AE,求矩形材料的面积。(2)、能否数出比(1)中更大面积的矩形材料?如果能,求出这些矩形材料面积的最大值;如果不能,说明理由.14. 已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4)(1)、求b,c满足的关系式(2)、设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式(3)、若该函数的图象不经过第三象限,当-5sx≤1时,函数的最大值与最小值之差为16,求b的值15. 设二次函数y=(x-x1)(x-x2)(x1 , x2是实数)。(1)、甲求得当x=0时,y=0;当x=1时,y=0;乙求得当x= 时,y=- ,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.(2)、写出二次函数图象的对称轴,并求该函数的最小值(用含x1 , x2的代数式表示).(3)、已知二次函数的图象经过(0,m)和(1,n)两点(m.n是实数)当0<x1<x2<1时,求证:0<mn< .16. 如图,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴,y轴的正半轴上,把正方形OABC的内部及边上,横,纵坐标均为整数的点称为好点,点P为抛物线y=-(x-m)2+m+2的顶点。
(1)、若所截矩形材料的一条边是BC或AE,求矩形材料的面积。(2)、能否数出比(1)中更大面积的矩形材料?如果能,求出这些矩形材料面积的最大值;如果不能,说明理由.14. 已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4)(1)、求b,c满足的关系式(2)、设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式(3)、若该函数的图象不经过第三象限,当-5sx≤1时,函数的最大值与最小值之差为16,求b的值15. 设二次函数y=(x-x1)(x-x2)(x1 , x2是实数)。(1)、甲求得当x=0时,y=0;当x=1时,y=0;乙求得当x= 时,y=- ,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.(2)、写出二次函数图象的对称轴,并求该函数的最小值(用含x1 , x2的代数式表示).(3)、已知二次函数的图象经过(0,m)和(1,n)两点(m.n是实数)当0<x1<x2<1时,求证:0<mn< .16. 如图,在平面直角坐标系中,正方形OABC的边长为4,边OA,OC分别在x轴,y轴的正半轴上,把正方形OABC的内部及边上,横,纵坐标均为整数的点称为好点,点P为抛物线y=-(x-m)2+m+2的顶点。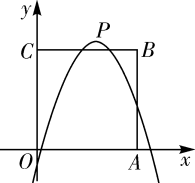 (1)、当m=0时,求该抛物线下方(包括边界)的好点个数。(2)、当m=3时,求该抛物线上的好点坐标。(3)、若点P在正方形OABC内部,该抛物线下方(包括边界)给好存在8个好点,求m的取值范围,
(1)、当m=0时,求该抛物线下方(包括边界)的好点个数。(2)、当m=3时,求该抛物线上的好点坐标。(3)、若点P在正方形OABC内部,该抛物线下方(包括边界)给好存在8个好点,求m的取值范围,
-