2019年浙江省中考数学分类汇编专题03：方程与不等式

试卷更新日期：2019-07-11 类型：二轮复习

进入出卷网下载

一、单选题

1. 不等式 $\frac{3 - x}{2}$ $> x$ 的解为（）

A、 $x < 1$ B、 $x < - 1$ C、 $x > 1$ D、 $x > - 1$

查看试题解析
2. 某商品经过连续两次降价，售价由原来的每件25元降到每件16元，则平均每次降价的百分率为（）．

A、20% B、40% C、18% D、36%

查看试题解析
3. 方程 $\frac{2}{3 x - 1}$ = $\frac{3}{x}$ 的解为（）．

A、x= $\frac{3}{11}$ B、x= $\frac{11}{3}$ C、x= $\frac{3}{7}$ D、x= $\frac{7}{3}$

查看试题解析
4. 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两(我国古代货币单位)；马三匹、牛五头，共价三十八两．问马、牛各价几何?”设马每匹 $x$ 两，牛每头 $y$ 两，根据题意可列方程组为（）

A、 ${\begin{cases} 4 x + 6 y = 38 \\ 3 x + 5 y = 48 \end{cases}$ B、 ${\begin{cases} 4 y + 6 x = 48 \\ 3 y + 5 x = 38 \end{cases}$ C、 ${\begin{cases} 4 x + 6 y = 48 \\ 5 x + 3 y = 38 \end{cases}$ D、 ${\begin{cases} 4 x + 6 y = 48 \\ 3 x + 5 y = 38 \end{cases}$

查看试题解析
5. 已知四个实数 $a$ ， $b$ ， $c$ ， $d$ ，若 $a > b$ ， $c > d$ ，则（）

A、 $a + c > b + d$ B、 $a - c > b - d$ C、 $a c > b d$ D、 $\frac{a}{c} > \frac{b}{d}$

查看试题解析
6. 如图是一个2×2的方阵，其中每行、每列的两数和相等，则 $a$ 可以是（）

$\sqrt[3]{8}$

2⁰

a

$| - 2 |$

A、 $\tan 60^{\circ}$ B、-1 C、0 D、 $1^{2019}$

查看试题解析

7. 一道来自课本的习题：

从甲地到乙地有一段上坡与一段平路，如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54min，从乙地到甲地需42min，甲地到乙地全程是多少？

小红将这个实际问题转化为二元一次方程组问题，设未知数x，y，已经列出一个方程 $\frac{x}{3} + \frac{y}{4} = \frac{54}{60}$ ，则另一个方程正确的是（）

A、

\frac{x}{4} + \frac{y}{3} = \frac{42}{60}

B、

\frac{x}{5} + \frac{y}{4} = \frac{42}{60}

C、

\frac{x}{4} + \frac{y}{5} = \frac{42}{60}

D、

\frac{x}{3} + \frac{y}{4} = \frac{42}{60}

查看试题解析

8. 已知九年级某班30位学生种树72株，男生每人种3棵树，女生每人种2棵树.设男生有x人，则（）

A、2x+3（72-x）=30 B、3x+2（72-x）=30 C、2x+3（30-x）=72 D、3x+2（30-x）=72

查看试题解析
9. 能说明命题“关于x的方程x²-4x+m=0一定有实数根”是假命题的反例为（）

A、m=-1 B、m=0 C、m=4 D、m=5

查看试题解析
10. 小慧去花店购买鲜花，若买5支玫瑰和3支百合，则她所带的钱还剩下10元；若买3支玫瑰和5支百合，则她所带的钱还缺4元.若只买8支玫瑰，则她所带的钱还剩下（）

A、31元 B、30元 C、25元 D、19元

查看试题解析

二、填空题

11. 不等式组 ${\begin{cases} x + 2 > 3 \\ \frac{x - 1}{2} \leq 4 \end{cases}$ 的解为．

查看试题解析
12. 不等式组 ${\begin{cases} \frac{3 - x}{2} \leq 0 \\ 3 x + 2 \geq 1 \end{cases}$ 的解集是。

查看试题解析
13. 在x²+ +4=0的括号中添加一个关于x的一次项，使方程有两个相等的实数根。

查看试题解析
14. 在 $x^{2} + () + 4 = 0$ 的括号中添加一个关于 $x$ 的一次项，使方程有两个相等的实数根

查看试题解析
15. 不等式3x-2≥4的解为.

查看试题解析

三、解答题

16.

(1)、计算:4sin60°+(π-2)⁰-( $- \frac{1}{2}$ )- $\sqrt{12}$

(2)、x为何值时，两个代数式x²+1，4x+1的值相等？

查看试题解析
17. 某旅行团32人在景区A游玩，他们由成人、少年和儿童组成．已知儿童10人，成人比少年多12人．

(1)、求该旅行团中成人与少年分别是多少人?

(2)、因时间充裕，该团准备让成人和少年（至少各1名）带领10名儿童去另一景区B游玩．景区B的门票价格为100元/张，成人全票，少年8折，儿童6折，一名成人可以免费携带一名儿童．①若由成人8人和少年5人带队，则所需门票的总费用是多少元?②若剩余经费只有1200元可用于购票，在不超额的前提下，最多可以安排成人和少年共多少人带队?求所有满足条件的方案，并指出哪种方案购票费用最少．

查看试题解析
18. 寒梅中学为了丰富学生的课余生活，计划购买围棋和中国象棋供棋类兴趣小组活动使用。若购买3副围棋和5副中国象棋需用98元；若购买8副围棋和3副中国象棋需用158元．

(1)、求每副围棋和每副中国象棋各多少元；

(2)、寒梅中学决定购买围棋和中国象棋共40副，总费用不超过550元，那么寒梅中学最多可以购买多少副围棋?

查看试题解析
19. 某风景区内的公路如图1所示，景区内有免费的班车，从入口处出发，沿该公路开往草甸，途中停靠塔林（上下车时间忽略不计）.第一班车上午8点发车，以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩，上午7：40到达入口处，因还没到班车发车时间，于是从景区入口处出发，沿该公路步行25分钟后到达塔林。离入口处的路程y（米）与时间x（分)的函数关系如图2所示.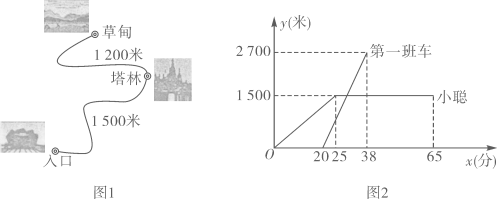

(1)、求第一班车离入口处的路程y（米）与时间x（分）的函数表达式

(2)、求第一班车从人口处到达塔林所蓄的时间。

(3)、小聪在塔林游玩40分钟后，想坐班车到草甸，则小聘最早能够坐上第几班车?如果他坐这班车到草甸，比他在塔林游玩结束后立即步行到草甸提早了几分钟?（假设每一班车速度均相同，小聪步行速度不变）

查看试题解析

$\sqrt[3]{8}$	2⁰
a	$\| - 2 \|$