河南省新乡市2019届高三文数第三次模拟测试试卷
试卷更新日期:2019-07-11 类型:高考模拟
一、单选题
-
1. ( )A、5 B、 C、6 D、2. 已知集合 ,则下列判断正确的是( )A、 B、 C、 D、3. 某超市抽取 袋袋装食用盐,对其质量(单位: )进行统计,得到如下茎叶图,若从这 袋食用盐中随机选取 袋,则该袋食用盐的质量在[499,501]内的概率为( )
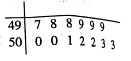 A、 B、 C、 D、4. 设向量 , 是平面内的一组基底,若向量 与 共线,则 ( )A、 B、 C、 D、5. 已知函数 为偶函数,当 时, ,则( )A、 B、 C、 D、6. 若曲线 在点 处的切线的斜率为 ,则 ( )A、 B、 C、 D、7. 如图,过双曲线 的右焦点 作 轴的垂线交 于 两点( 在 的上方),若 到 的一条渐近线的距离分别为 ,且 ,则 的离心率为( )
A、 B、 C、 D、4. 设向量 , 是平面内的一组基底,若向量 与 共线,则 ( )A、 B、 C、 D、5. 已知函数 为偶函数,当 时, ,则( )A、 B、 C、 D、6. 若曲线 在点 处的切线的斜率为 ,则 ( )A、 B、 C、 D、7. 如图,过双曲线 的右焦点 作 轴的垂线交 于 两点( 在 的上方),若 到 的一条渐近线的距离分别为 ,且 ,则 的离心率为( )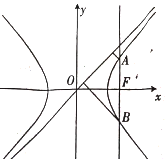 A、 B、 C、 D、8. 已知函数 ,若 的最小正周期为 ,且 ,则 的解析式为( )A、 B、 C、 D、9. 已知等比数列 的前 项和为 ,且 ,则 ( )A、 B、 C、 D、10. 若圆 与圆 的公共弦长为 ,则圆 的半径为( )A、 B、 C、 D、11. 某几何体由一个棱柱与一个棱锥组合而成,其三视图如图所示,其中俯视图和侧视图中的正方形的边长为2,正视图和俯视图中的三角形均为等腰直角三角形,则该几何体的体积为( )
A、 B、 C、 D、8. 已知函数 ,若 的最小正周期为 ,且 ,则 的解析式为( )A、 B、 C、 D、9. 已知等比数列 的前 项和为 ,且 ,则 ( )A、 B、 C、 D、10. 若圆 与圆 的公共弦长为 ,则圆 的半径为( )A、 B、 C、 D、11. 某几何体由一个棱柱与一个棱锥组合而成,其三视图如图所示,其中俯视图和侧视图中的正方形的边长为2,正视图和俯视图中的三角形均为等腰直角三角形,则该几何体的体积为( )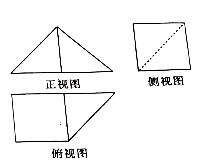 A、 B、 或 C、 D、 或12. 已知函数 ,若关于 的方程 只有两个不同的实根,则 的取值范围为( )
A、 B、 或 C、 D、 或12. 已知函数 ,若关于 的方程 只有两个不同的实根,则 的取值范围为( )
A、 B、 C、 D、二、填空题
-
13. 在样本的频率分布直方图中,共有 个小长方形,若中间一个长方形的面积等于其他 个小长方形面积的和的 ,且样本容量为 ,则中间一组的频数为 .14. 记等差数列 的前 项和为 ,若 ,则 .15. 在正方体 中, 为棱 上一点,且 , 为棱 的中点,且平面 与 交于点 ,则 与平面 所成角的正切值为 .16. 某农户计划种植莴笋和西红柿,种植面积不超过 亩,投入资金不超过 万元,假设种植莴笋和西红柿的产量、成本和售价如下表:
年产量/亩
年种植成本/亩
每吨售价
莴笋
5吨
1万元
0.5万元
西红柿
4.5吨
0.5万元
0.4万元
那么,该农户一年种植总利润(总利润=总销售收入-总种植成本)的最大值为万元
三、解答题
-
17. 在平面四边形 中, , , , .
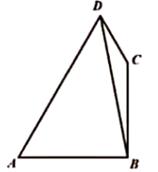 (1)、求 ;(2)、若 ,求 .18. 《最强大脑》是江苏卫视引进德国节目《Super Brain》而推出的大型科学竞技真人秀节目,节目筹备组透露挑选选手的方式:不但要对空间感知、照相式记忆进行考核,而且要让选手经过名校最权威的脑力测试, 分以上才有机会入围,某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各 名,然后对这 名学生进行脑力测试,规定:分数不小于 分为“入围学生”,分数小于 分为“未入围学生”,已知男生入围 人,女生未入围 人,(1)、根据题意,填写下面的 列联表,并根据列联表判断是否有 以上的把握认为脑力测试后是否为“入围学生”与性别有关.
(1)、求 ;(2)、若 ,求 .18. 《最强大脑》是江苏卫视引进德国节目《Super Brain》而推出的大型科学竞技真人秀节目,节目筹备组透露挑选选手的方式:不但要对空间感知、照相式记忆进行考核,而且要让选手经过名校最权威的脑力测试, 分以上才有机会入围,某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各 名,然后对这 名学生进行脑力测试,规定:分数不小于 分为“入围学生”,分数小于 分为“未入围学生”,已知男生入围 人,女生未入围 人,(1)、根据题意,填写下面的 列联表,并根据列联表判断是否有 以上的把握认为脑力测试后是否为“入围学生”与性别有关.性别
入围人数
未入围人数
总计
男生
24
女生
80
总计
(2)、用分层抽样的方法从“入围学生”中随机抽取 名学生.(ⅰ)求这 名学生中女生的人数;
(ⅱ)若抽取的女生的脑力测试分数各不相同(每个人的分数都是整数),求这 名学生中女生测试分数的平均分的最小值.
附: ,其中
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
19. 如图,三棱柱 各条棱长均为 ,且 平面 , 为 的中点, 分别在线段 和线段 上,且 ,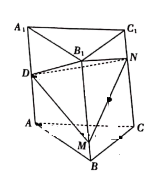 (1)、证明:平面 平面 ;(2)、求三棱锥 的体积.20. 已知直线 与椭圆 交于 两点, 与直线 交于点(1)、证明: 与C相切;(2)、设线段 的中点为 ,且 ,求 的方程.
(1)、证明:平面 平面 ;(2)、求三棱锥 的体积.20. 已知直线 与椭圆 交于 两点, 与直线 交于点(1)、证明: 与C相切;(2)、设线段 的中点为 ,且 ,求 的方程.