河南省六市2019届高三理数第二次联考试卷
试卷更新日期:2019-07-11 类型:高考模拟
一、单选题
-
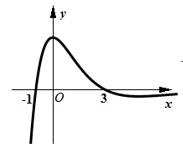
1. 已知集合 ,集合 ,则集合 等于( )A、 B、 C、 D、2. 若复数 满足 ,则 的虚部为( )A、-4 B、 C、4 D、3. 某学校为落实学生掌握社会主义核心价值观的情况,用系统抽样的方法从全校2400名学生中抽取30人进行调查.现将2400名学生随机地从1~2400编号,按编号顺序平均分成30组(1~80号,81~160号,…,2321~2400号),若第3组与第4组抽出的号码之和为432,则第6组抽到的号码是( )A、416 B、432 C、448 D、4644. 等差数列 的公差为2,且 是 与 的等比中项,则该数列的前 项和 取最小值时,则 的值为( )A、7 B、6 C、5 D、45. 设 是正方体 的对角面 (含边界)内的点,若点 到平面 、平面 、平面 的距离相等,则符合条件的点 ( )A、仅有一个 B、有有限多个 C、有无限多个 D、不存在6. 已知 ,点 为斜边 的中点, , , ,则 等于( )A、-14 B、-9 C、9 D、147. 设变量 , 满足不等式组 ,则 的最大值为( )A、 B、 C、 D、68. 函数 的大致图象为( )A、
 B、
B、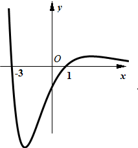 C、
C、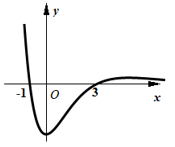 D、
D、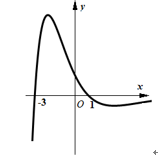 9. 设实数 分别满足 , , ,则 的大小关系为A、 B、 C、 D、10. 在直角坐标系 中, 是椭圆 的左焦点, 分别为左、右顶点,过点 作 轴的垂线交椭圆 于 两点,连接 交 轴于点 ,连接 交 于点 ,若 是线段 的中点,则椭圆 的离心率为( )A、 B、 C、 D、11. 已知数列 中, ,且对任意的 ,都有 ,则 ( )A、 B、 C、 D、12. 已知函数 的图象与直线 恰有三个公共点,这三个点的横坐标从小到大依次为 ,则 ( )A、-2 B、 C、0 D、1
9. 设实数 分别满足 , , ,则 的大小关系为A、 B、 C、 D、10. 在直角坐标系 中, 是椭圆 的左焦点, 分别为左、右顶点,过点 作 轴的垂线交椭圆 于 两点,连接 交 轴于点 ,连接 交 于点 ,若 是线段 的中点,则椭圆 的离心率为( )A、 B、 C、 D、11. 已知数列 中, ,且对任意的 ,都有 ,则 ( )A、 B、 C、 D、12. 已知函数 的图象与直线 恰有三个公共点,这三个点的横坐标从小到大依次为 ,则 ( )A、-2 B、 C、0 D、1二、填空题
-
13. 已知 , 是第三象限角,则 .14. 《易经》是中国传统文化中的精髓,下图是易经八卦图(含乾、坤、巽、震、坎、离、艮、兑八卦),每卦有三根线组成(“
 ”表示一根阳线,“
”表示一根阳线,“  ”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率 .
”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率 .  15. 抛物线 的焦点为 ,其准线为直线 ,过点 作直线 的垂线,垂足为 ,则 的角平分线所在的直线斜率是 .16. 我国古代数学名著《九章算术》中有如下问题:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺。问积几何”,羡除是一个五面体,其中三个面是梯形,另两个面是三角形,已知一个羡除的三视图如图粗线所示,其中小正方形网格的边长为1,则该羡除的体积为 .
15. 抛物线 的焦点为 ,其准线为直线 ,过点 作直线 的垂线,垂足为 ,则 的角平分线所在的直线斜率是 .16. 我国古代数学名著《九章算术》中有如下问题:“今有羡除,下广六尺,上广一丈,深三尺,末广八尺,无深,袤七尺。问积几何”,羡除是一个五面体,其中三个面是梯形,另两个面是三角形,已知一个羡除的三视图如图粗线所示,其中小正方形网格的边长为1,则该羡除的体积为 .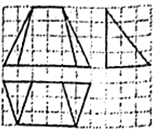
三、解答题
-
17. 在 中,内角 、 、 的对边分别为 、 、 ,且满足 .(1)、求 的值;(2)、若 ,求 的值.18. 如图,四棱锥 , , , , 为等边三角形,平面 平面 , 为 中点.
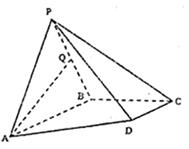 (1)、求证: 平面 ;(2)、求二面角 的余弦值.19. 为评估 设备生产某种零件的性能,从该设备生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
(1)、求证: 平面 ;(2)、求二面角 的余弦值.19. 为评估 设备生产某种零件的性能,从该设备生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:直径/
78
79
81
82
83
84
85
86
87
88
89
90
91
93
合计
件数
1
1
3
5
6
19
33
18
4
4
2
1
2
1
100
经计算,样本的平均值 ,标准差 ,以频率值作为概率的估计值.
(1)、为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为 ,并根据以下不等式进行评判( 表示相应事件的频率):① ;② ;③ ,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断 设备的性能等级.
(2)、将直径小于等于 的零件或直径大于等于 的零件认定为是“次品”,将直径小于等于 的零件或直径大于等于 的零件认定为是“突变品”,从样本的“次品”中随意抽取2件零件,求“突变品”个数 的数学期望.20. 已知动点 到定点 和到直线 的距离之比为 ,设动点 的轨迹为曲线 ,过点 作垂直于 轴的直线与曲线 相交于 、 两点,直线 : 与曲线 交于 、 两点,与 相交于一点(交点位于线段 上,且与 、 不重合).(1)、求曲线 的方程;(2)、当直线 与圆 相切时,四边形 的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.