山东省聊城市莘县2018-2019学年中考数学二模考试试卷

试卷更新日期：2019-07-10 类型：中考模拟

进入出卷网下载

一、选择题：（每小题3分，共36分）

1. 下列四个数中，是无理数的是（）

A、 $\frac{π}{2}$ B、 $\frac{22}{7}$ C、 $\sqrt[3]{- 8}$ D、（ $\sqrt{3}$ ）²

查看试题解析
2. 如图，直线L上有三个正方形a，b，c，若a，c的面积分别为1和9，则b的面积为（）

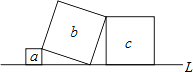A、8 B、9 C、10 D、11

查看试题解析
3. 如图是某个几何体的展开图，该几何体是（）

A、三棱柱 B、圆锥 C、四棱柱 D、圆柱

查看试题解析
4. 据有关部门统计，2018年“国庆小长假”期间，济南各大景点共接待游客约1442000人次，将数14420000用科学记数法表示为（）

A、1.42×10⁷ B、0.1442×10⁷ C、1.442×10⁸ D、0.1442×10⁸

查看试题解析
5. 如图，在矩形纸片ABCD中，AB=3，点E在边BC上，将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，若∠EAC=∠ECA，则AD的长是（）．

A、3 $\sqrt{3}$ B、6 C、4 D、5

查看试题解析
6. 用配方法解一元二次方程x²+4x-9=0时，原方程可变形为（）

A、(x+2)²=1 B、(x+2)²=7 C、(x+2)²=13 D、(x+2)²=19

查看试题解析
7. 下面四个图形分别是绿色食品、节水、节能和回收标志，在这四个标志中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为4的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D’处，则点C的对应点C'的坐标为（）

A、(2 $\sqrt{3}$ ，2） B、(4，2) C、（4，2 $\sqrt{3}$ ） D、（2，2 $\sqrt{3}$ ）

查看试题解析
9. 若不等式组 ${\begin{cases} 5 x + 1 \leq 3 x - 5 \\ 5 - x < k \end{cases}$ 无解，则k的取值范围是（）

A、k≤8 B、k<8 C、k>8 D、k≤4

查看试题解析
10. 关于x的分式方程 $\frac{x + m}{x - 2} + \frac{2 m}{2 - x} = 3$ 的解为非负实数，则实数m的取值范围是( ）

A、m=-6且m≠2 B、m≤6且m≠2 C、m≤-6且m≠-2 D、m<6且m≠2

查看试题解析
11. 如图，AB是圆O的直径，弦CD⊥AB，∠BCD=30°，CD=2 $\sqrt{3}$ 则S_阴影=（）

A、2π B、 $\frac{8}{3} π$ C、 $\frac{4}{3} π$ D、 $\frac{2}{3} π$

查看试题解析
12. 如图，抛物线y=-x²+2x+m+1交x轴于点A(a，0）和B(b，0），交y轴于点C，抛物线的顶点为D，下列四个判断：①当x>0时，y>0；②若a=-1，则b=3；③抛物线上有两点P(x₁ ， y₁）和Q（x₂ ， y₂），若x₁<1<x₂ ，且x₁+x₂>2，则y₁>y₂；④点C关于抛物线对称轴的对称点为E，点G、F分别在x轴和y轴上，当m=2时，四边形EDGF周长的最小值为 $\sqrt{58}$ ．其中，判断正确的序号是（）

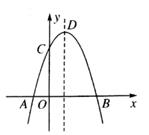A、①② B、②③ C、①③ D、②③④

查看试题解析

二、填空题（每题3分，共15分）

13. 已知一个正数的平方根是x和x-6，这个数是．

查看试题解析
14. 若不等式组 ${\begin{cases} 2 x - a < 1 \\ x - 2 b > 3 \end{cases}$ 的解集是-3<x<1，则a+b= ．

查看试题解析
15. 如图，在平面直角坐标系中，将长方形AOCD沿直线AE折叠（点E在边DC上），折叠后顶点D恰好落在边OC上的点F处，若点D的坐标为（10，8)，则点E的纵坐标为。

查看试题解析
16. 在一个不透明的袋子里装有4个球（仅颜色不同），其中3个是红球，1个是白球，从中任意摸出一个球，记下颜色后放回，搅匀，再任意摸出一个球，则两次摸出都是红球的概率是。

查看试题解析
17. 在直角坐标系中，直线l：y= $\frac{\sqrt{3}}{3} x - \frac{\sqrt{3}}{3}$ 与x轴交于点B，以OB₁为边长作等边△A₁OB₁ ，过点A1作A₁B₂平行于x轴，交直线l于点B₂ ，以A₁B₂为边长作等边△A₂A₁B₂ ，过点A₂作A₁B₂平行于x轴，交直线l于点B₃ ，以A₂B₃为边长作等边△A₃A₂B₃ ． …，则等边△A₂₀₁₉A₂₀₁₈B₂₀₁₉的边长是．

查看试题解析

三、解答题（本大题共8小题，共69分）

18. 先化简： $(\frac{1}{x - 1} - \frac{1}{x + 1}) \div \frac{x + 2}{x^{2} - 1}$ ，再从-2，-1,0，1这四个数中选择一个合适的数代入求值。

查看试题解析
19. 某公司在农业示范基地采购A，B两种农产品，已知A种农产品每千克的进价比B种多2元，且用24000元购买A种农产品的数量（按重量计）与用18000元购买B种农产品的数量（按重量计）相同。

(1)、求A，B两种农产品每千克的进价分别是多少元?

(2)、该公司计划购进A，B两种农产品共40吨，并运往异地销售，运费为500元/吨，已知A种农产品售价为15元/kg，B种农产品售价为12元/kg，其中A种农产品至少购进15吨且不超过B种农产品的数量，问该公司应如何采购才能获得最大利润，最大利润是多少？

查看试题解析
20. 如图，矩形ABCD的对角线AC，BD相交于点O，过点A作BD的平行线交CD的延长线于点E．

(1)、求证：AE=AC；

(2)、若AE=5，DE=3，连接OE，求tan∠OEC的值．

查看试题解析
21. d 大课间活动中，同学们积极参加体育锻炼，小明就本班同学“我最喜爱的体育项目“进行了一次调查统计，下面是他通过收集数据后，绘制的两幅不完整的统计图．
请你根据图中提供的信息，解答以下问题：

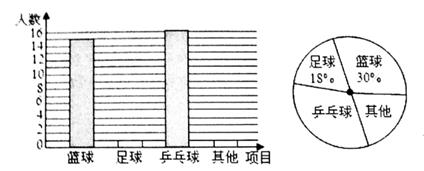(1)、该班共有名学生；

(2)、补全条形统计图：

(3)、在扇形统计图中，“乒乓球”部分所对应的圆心角度数为；

(4)、学校将举办体育节，该班将推选5位同学参加乒乓球活动，有3位男同学(A，B，C)
和2位女同学（D，E)，现准备从中选取两名同学组成双打组合，用树状图或列表法求恰好选出一男一女组成双打组合的概率。

查看试题解析
22. 如图，在大楼AB的正前方有一斜坡CD，CD=13米，坡度为1： $\frac{12}{5}$ ，高为DE，在斜坡下的点C处测得楼顶B的仰角为64°，在斜坡上的点D处测得楼顶B的仰角为45°，其中A、C、E在同一直线上．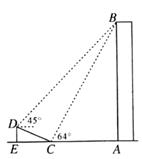

(1)、求斜坡CD的高度DE；

(2)、求大楼AB的高度；（参考数据：sin64°≈0.9，tan64°≈2)．

查看试题解析
23. 如图，一次函数y=kx+b与反比例函数y= $\frac{6}{x}$ （x>0）的图象交于A(m，6），B(3，n)两点

(1)、求一次函数的解析式；

(2)、根据图象直接写出使kx+b< $\frac{6}{x}$ 成立的x的取值范围；

(3)、求△AOB的面积

查看试题解析
24. 如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以边BC为直径作⊙O，交AB于D，DE是⊙O的切线，过点B作DE的垂线，垂足为E．

(1)、求证：∠ABC=∠ABE；

(2)、求DE的长．

查看试题解析
25. 如图，抛物线y=-x²+bx+c交x轴于点A（-3，0)和点B，交y轴于点C(0，3）．

(1)、求抛物线的函数表达式；

(2)、若点P在抛物线上，且S_△AOP=4S_△BOC ，求点P的坐标；

(3)、如图b，设点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ长度的最大值，并求出△DAC面积的最大值．

查看试题解析