山东省邹平县2018-2019学年中考数学四模考试试卷
试卷更新日期:2019-07-10 类型:中考模拟
一、选择题:本大题共12个小题,每小题3分,满分36分.
-
1. 2018年我国在人工智能领域取得显著成就,自主研发的人工智能“绝艺”获得全球最前沿的人工智能赛事冠军,这得益于所建立的大数据中心的规模和数据存储量,它们决定着人工智能深度学习的质量和速度,其中的一个大数据中心能存储58000000000本书籍.将58000000000用科学记数法表示应为( )A、58×109 B、5.8×1010 C、5.8×1011 D、0.58×10112. 下列计算正确的是( )A、a2+a2=a4 B、(-a3)2=-a6 C、a3·a2=a6 D、a5÷a2=a33. 如图,由4个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
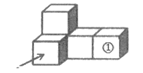 A、主视图不变,左视图改变 B、主视图不变,左视图不变 C、主视图改变,左视图不变 D、主视图改变,左视图改变4. 如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD的度数为( )
A、主视图不变,左视图改变 B、主视图不变,左视图不变 C、主视图改变,左视图不变 D、主视图改变,左视图改变4. 如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD的度数为( ) A、110° B、120° C、125° D、135°5. 下列图形中,∠B=2∠A的是( )A、
A、110° B、120° C、125° D、135°5. 下列图形中,∠B=2∠A的是( )A、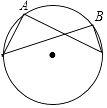 B、
B、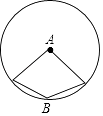 C、
C、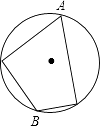 D、
D、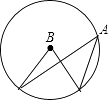 6. 如图所示图形中,既是轴对称图形,又是中心对称图形的是( )A、
6. 如图所示图形中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 不等式组 的解集在数轴上表示正确的是( )A、
7. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、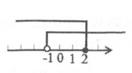 C、
C、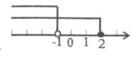 D、
D、 8. 在一次期末考试中,学校为了解初二学生的数学水平,随机抽取了部分学生的数学成绩,并计算了他们的样本方差S2=[(95-70)2+(67-70)2+…+(92-70)2],请问这次抽取的学生人数及这些学生的平均成绩分别是( )
8. 在一次期末考试中,学校为了解初二学生的数学水平,随机抽取了部分学生的数学成绩,并计算了他们的样本方差S2=[(95-70)2+(67-70)2+…+(92-70)2],请问这次抽取的学生人数及这些学生的平均成绩分别是( )
A、60,60 B、70,70 C、60,70 D、70,609. 一元二次方程mx2+mx- =0有两个相等实数根,则m的值为( )A、0 B、0或-2 C、-2 D、210. 如图,小明站在自家阳台上A处观测到对面大楼底部C的俯角为a,A处到地面B处的距离AB=35m,则两栋楼之间的距离BC(单位:m)为( )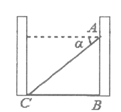 A、35tanα B、35sinα C、 D、11. 直线y=- x+ 与x轴,y轴交于A、B两点,若把△AB0沿直线AB翻折,点O
A、35tanα B、35sinα C、 D、11. 直线y=- x+ 与x轴,y轴交于A、B两点,若把△AB0沿直线AB翻折,点O落在第一象限的C处,则C点的坐标为( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中2条直线为l1:y=-3x+3,2:y=-3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中: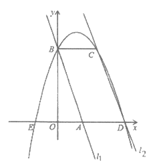
①a-b+c=0;②2a+b+c=5;③抛物线关于直线x=1对称;④抛物线过点(b,c);⑤S四边形ABCD=5.其中正确的个数有( )
A、5 B、4 C、3 D、2二、填空题:本大题共8个小题,每小题5分,满分40分.
-
13. 分解因式:3x3-27x=.14. 已知二元一次方程组 ,则x-y= .15. 分式方程 的解为 。
16. 如图是两个质地均匀的转盘,现转动转盘①和转盘②各一次,则两个转盘指针都指向红的部分的概率为。 17. 如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为 .
17. 如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为 . 18. 如图,过点A(3,4)作AB⊥x轴,垂足为B,交反比例函数y= 的图象于点C(x1 ,
18. 如图,过点A(3,4)作AB⊥x轴,垂足为B,交反比例函数y= 的图象于点C(x1 ,y1),连接0A交反比例函数y= 的图象于点D(2,y2),则y2-y1= .
 19. 如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG的最小值为 .
19. 如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG的最小值为 .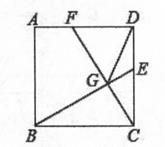 20. 如图,在直角坐标系中,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时,反射角等于入射角,当小球第1次碰到矩形的边时的点为P1 , 第2次碰到矩形的边时的点为P2 , …,第n次碰到矩形的边时的点为Pn,则点P2019的坐标是 .
20. 如图,在直角坐标系中,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时,反射角等于入射角,当小球第1次碰到矩形的边时的点为P1 , 第2次碰到矩形的边时的点为P2 , …,第n次碰到矩形的边时的点为Pn,则点P2019的坐标是 .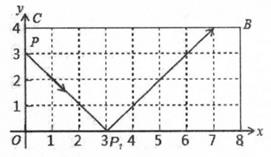
三、解答题:本大题共6个小题,满分74分.
-
21. 已知代数式((1)、先化简,再求当x=3时,原代数式的值;(2)、原代数式的值能等于-1吗?为什么?22. 2018年5月13日,大国重器—一中国第一艘国产航母正式海试,某校团支部为了了解同学们对此事的知晓情况,随机抽取了部分同学进行调查,并根据收集到的信息绘制了如下两幅不完整的统计图,图中A表示“知道得很详细”,B表示“知道个大概”,C表示“听说了”,D表示“完全不知道”,请根据途中提供的信息完成下列问题:
 (1)、扇形统计图中A对应的圆心角是多少度,并补全折线统计图.(2)、被抽取的同学中有4位同学都是班级的信息员,其中有一位信息员属于D类,校团支部从这4位信息员中随机选出两位作为校广播站某访谈节目的嘉宾,请用列表法或画树状图法,求出属于D类的信息员被选为的嘉宾的概率。23. 如图,在直角坐标系xOy中,直线y= x+b经过点A(-3,0)与y轴正半轴交于B点,在x轴正半轴上有一点D,且OA=OD,过D点作DC⊥x轴交直线y= x+b于C点,反比例函数y= (x>0)的图象经过点C.
(1)、扇形统计图中A对应的圆心角是多少度,并补全折线统计图.(2)、被抽取的同学中有4位同学都是班级的信息员,其中有一位信息员属于D类,校团支部从这4位信息员中随机选出两位作为校广播站某访谈节目的嘉宾,请用列表法或画树状图法,求出属于D类的信息员被选为的嘉宾的概率。23. 如图,在直角坐标系xOy中,直线y= x+b经过点A(-3,0)与y轴正半轴交于B点,在x轴正半轴上有一点D,且OA=OD,过D点作DC⊥x轴交直线y= x+b于C点,反比例函数y= (x>0)的图象经过点C. (1)、求b和k的值;(2)、反比例函数图象上是否存在点P,使四边形BCPD为菱形?如果存在,求出P的点坐标;如果不存在,说明理由.24. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)、求b和k的值;(2)、反比例函数图象上是否存在点P,使四边形BCPD为菱形?如果存在,求出P的点坐标;如果不存在,说明理由.24. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F. (1)、求证:△DAE≌△CFE;(2)、若AB=BC+AD,求证:BE⊥AF;(3)、在(2)的条件下,若∠D=90°,AD= ,AF=10,则点E到AB的距离是(直接写出结果即可,不用写出演推过程)25. 如图,在平面直角坐标系中, ABCD的边AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>0B.
(1)、求证:△DAE≌△CFE;(2)、若AB=BC+AD,求证:BE⊥AF;(3)、在(2)的条件下,若∠D=90°,AD= ,AF=10,则点E到AB的距离是(直接写出结果即可,不用写出演推过程)25. 如图,在平面直角坐标系中, ABCD的边AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>0B. (1)、求OA、OB的长.(2)、若x轴上的有一个点E满足S△AOE= ,求证:△AOE∽△AOD.(3)、在直线AB上是否存在点F,使以A、C、F为顶点的三角形是等腰三角形?如果存在,请直接写出所有满足要求的点F的坐标。26. 如图1,在平面直角坐标系xOy中,直线l:y= x+m与x轴、y轴分别交于点A和点B(0,-1),抛物线y= x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)、求OA、OB的长.(2)、若x轴上的有一个点E满足S△AOE= ,求证:△AOE∽△AOD.(3)、在直线AB上是否存在点F,使以A、C、F为顶点的三角形是等腰三角形?如果存在,请直接写出所有满足要求的点F的坐标。26. 如图1,在平面直角坐标系xOy中,直线l:y= x+m与x轴、y轴分别交于点A和点B(0,-1),抛物线y= x2+bx+c经过点B,与直线l的另一个交点为C(4,n). (1)、求n的值和抛物线的解析式;(2)、点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;(3)、M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1 , 点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.
(1)、求n的值和抛物线的解析式;(2)、点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;(3)、M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1 , 点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.