山东省德州市乐陵市2018-2019学年中考数学模拟考试试卷
试卷更新日期:2019-07-10 类型:中考模拟
一、选择题:本大题共12小题,每小题4分,共48分.
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 下面四个应用图标中,既是轴对称图形又是中心对称图形的是( )A、
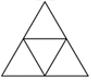 B、
B、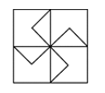 C、
C、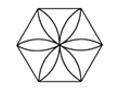 D、
D、 3. 2018年4月18日,被誉为“中国天眼”的FAST望远镜首次发现的毫秒脉冲星得到国际认证.新发现的脉冲星自转周期为0.00519秒,是至今发现的射电流量最弱的高能毫秒脉冲星之一.将0.00519用科学记数法表示应为( )A、 B、 C、 D、4. 下列图形能折叠成三棱柱的是( )A、
3. 2018年4月18日,被誉为“中国天眼”的FAST望远镜首次发现的毫秒脉冲星得到国际认证.新发现的脉冲星自转周期为0.00519秒,是至今发现的射电流量最弱的高能毫秒脉冲星之一.将0.00519用科学记数法表示应为( )A、 B、 C、 D、4. 下列图形能折叠成三棱柱的是( )A、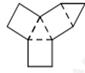 B、
B、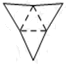 C、
C、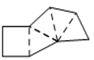 D、
D、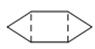 5. 若代数式 有意义,则实数 的取值范围是( )
5. 若代数式 有意义,则实数 的取值范围是( )
A、 B、 C、 D、6. 如图圆O是等边△ABC的外接圆,其半径为3. 则阴影部分的面积是( )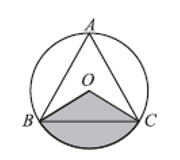 A、 B、 C、 D、7. 第24届冬奥会将于2022年在北京和张家口举行.冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有5张形状、大小、质地均相同的卡片,正面分别印有跳台滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的项目图案,背面完全相同.现将这5张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪图案的概率是( )
A、 B、 C、 D、7. 第24届冬奥会将于2022年在北京和张家口举行.冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有5张形状、大小、质地均相同的卡片,正面分别印有跳台滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的项目图案,背面完全相同.现将这5张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪图案的概率是( ) A、 B、 C、 D、8. 将 分解因式,所得结果正确的是( )A、 B、 C、 D、9. “单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中 四位同学的单词记忆效率 与复习的单词个数 的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
A、 B、 C、 D、8. 将 分解因式,所得结果正确的是( )A、 B、 C、 D、9. “单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中 四位同学的单词记忆效率 与复习的单词个数 的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )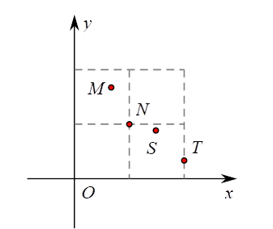 A、 B、 C、 D、10. 甲、乙两位同学做中国结,已知甲每小时比乙少做6个,甲做30个所用的时间与乙做45个所用的时间相同,求甲每小时做中国结的个数. 如果设甲每小时做x个,那么可列方程为 ( )A、 B、 C、 D、11. 已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A、 B、 C、 D、10. 甲、乙两位同学做中国结,已知甲每小时比乙少做6个,甲做30个所用的时间与乙做45个所用的时间相同,求甲每小时做中国结的个数. 如果设甲每小时做x个,那么可列方程为 ( )A、 B、 C、 D、11. 已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A、当a=1时,函数图象经过点(﹣1,1) B、当a=﹣2时,函数图象与x轴没有交点 C、若a<0,函数图象的顶点始终在x轴的下方 D、若a>0,则当x≥1时,y随x的增大而增大12. 如图所示,△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,正方形DEFG的边长也为2,且AC与DE在同一直线上,△ABC从C点与D点重合开始,沿直线DE向右平移,直到点A与点E重合为止,设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )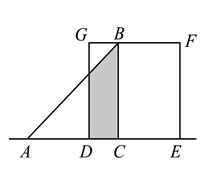 A、
A、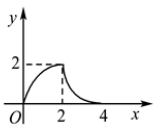 B、
B、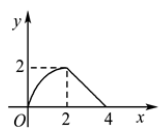 C、
C、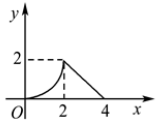 D、
D、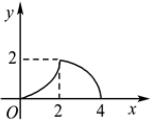
二、填空题:本大题共6小题,共24分,只填最后结果,每小题填对得4分.
-
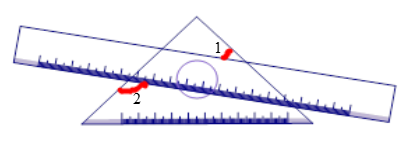
13. 已知 是方程组 的解,则a2﹣b2= .14. 将一把直尺与一块含45度的三角板如图放置,若 ,则 的度数为
 15. 把方程 用配方法化为 的形式,则m= , n= .16. 袋子中有20个除颜色外完全相同的小球. 在看不到球的条件下,随机地从袋子中摸出一个球,记录颜色后放回,将球摇匀. 重复上述过程150次后,共摸到红球30次,由此可以估计口袋中的红球个数是。17. 将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n个图形中“○”的个数是78,则n的值是
15. 把方程 用配方法化为 的形式,则m= , n= .16. 袋子中有20个除颜色外完全相同的小球. 在看不到球的条件下,随机地从袋子中摸出一个球,记录颜色后放回,将球摇匀. 重复上述过程150次后,共摸到红球30次,由此可以估计口袋中的红球个数是。17. 将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n个图形中“○”的个数是78,则n的值是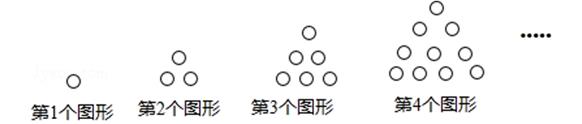 18. 定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.
18. 定义:圆中有公共端点的两条弦组成的折线称为圆的一条折弦.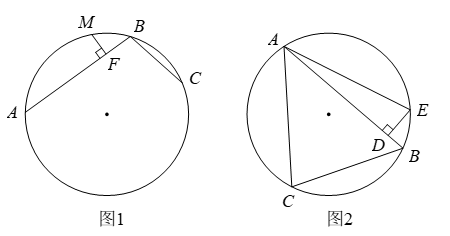
阿基米德折弦定理:如图1, 和 组成圆的折弦, , 是弧 的中点, 于 ,则 .
如图2,△ 中, , , , 是 上一点, ,作 交△ 的外接圆于 ,连接 ,则 =°.
三、解答题:本大题共7小题共78分.解答要写出必要的文字说明、证明过程或演算步骤.
-
19. 解不等式组: ,并写出它的所有整数解.20. 某校九年级八个班共有280名学生,男女生人数大致相同,调查小组为调查学生的体质健康水平,近期开展了一次调查研究,请将下面的过程补全.(1)、收集数据:
调查小组计划选取40名学生的体质健康测试成绩作为样本,下面的取样方法中,合理的是___________(填字母);
A、抽取九年级1班、2班各20名学生的体质健康测试成绩组成样本 B、抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本 C、从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本(2)、整理、描述数据:抽样方法确定后,调查小组获得了40名学生的体质健康测试成绩如下:
77 83 80 64 86 90 75 92 83 81 85 86 88 62 65 86 97 96 82 73
86 84 89 86 92 73 57 77 87 82 91 81 86 71 53 72 90 76 68 78
整理数据,如下表所示,请补充表格
2019年九年级部分学生体质健康测试成绩统计表
50≤x
<55
55≤x
<60
60≤x
<65
65≤x
<70
70≤x
<75
75≤x
<80
80≤x
<85
85≤x
<90
90≤x
<95
95≤x
<100
1
1
2
2
4
5
5
2
(3)、分析数据、得出结论:
调查小组将统计后的数据与去年同期九年级的学生的体质健康测试成绩(直方图)进行了对比,
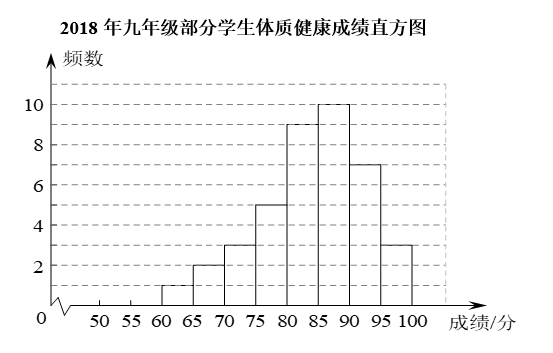
你能从中得到的结论是 , 你的理由是.
体育老师计划根据2019年的统计数据安排75分以下的同学参加体质加强训练项目,则全年级约有名同学参加此项目.
21. 在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.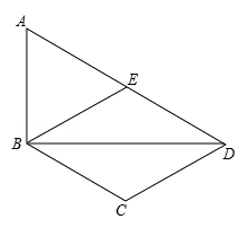 (1)、求证:四边形BCDE为菱形;(2)、连接AC,若AC平分∠BAD,BC=1,求AC的长.22. 如图,在⊙O中,C , D分别为半径OB , 弦AB的中点,连接CD并延长,交过点A的切线于点E .
(1)、求证:四边形BCDE为菱形;(2)、连接AC,若AC平分∠BAD,BC=1,求AC的长.22. 如图,在⊙O中,C , D分别为半径OB , 弦AB的中点,连接CD并延长,交过点A的切线于点E .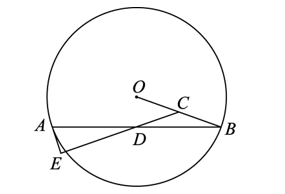 (1)、求证:AE⊥CE .(2)、若AE= ,sin∠ADE= ,求⊙O半径的长.23. 如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A、B,与反比例函数 的图象在第四象限交于点C,CD⊥x轴于点D,tan∠OAB=2,OA=2,OD=1.
(1)、求证:AE⊥CE .(2)、若AE= ,sin∠ADE= ,求⊙O半径的长.23. 如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A、B,与反比例函数 的图象在第四象限交于点C,CD⊥x轴于点D,tan∠OAB=2,OA=2,OD=1. (1)、求该反比例函数的表达式;(2)、点M是这个反比例函数图象上的点,过点M作MN⊥y轴,垂足为点N,连接OM、AN,如果S△ABN=2S△OMN , 直接写出点M的坐标.24. 问题背景:如图,在▱ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)、求该反比例函数的表达式;(2)、点M是这个反比例函数图象上的点,过点M作MN⊥y轴,垂足为点N,连接OM、AN,如果S△ABN=2S△OMN , 直接写出点M的坐标.24. 问题背景:如图,在▱ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.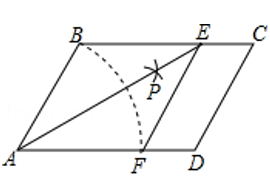 (1)、根据以上尺规作图的过程,求证:四边形ABEF是菱形;(2)、若菱形ABEF的周长为16,AE=4 ,求∠C的大小.25. 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)、根据以上尺规作图的过程,求证:四边形ABEF是菱形;(2)、若菱形ABEF的周长为16,AE=4 ,求∠C的大小.25. 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D. (1)、求二次函数的表达式;(2)、在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)、有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从 点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,△MNB面积最大,试求出最大面积.
(1)、求二次函数的表达式;(2)、在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)、有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从 点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,△MNB面积最大,试求出最大面积.