山东省滨州市2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2019-07-10 类型:期中考试
一、选择题
-
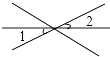
1. 下列图形中,∠1与∠2是对顶角的有( )A、
 B、
B、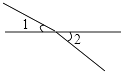 C、
C、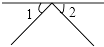 D、
D、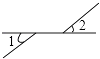 2. 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )
2. 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )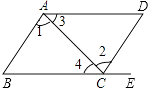 A、①④ B、②③ C、①③ D、①③④3. 下列各项中,不是由平移设计的是( )A、
A、①④ B、②③ C、①③ D、①③④3. 下列各项中,不是由平移设计的是( )A、 B、
B、  C、
C、 D、
D、 4. 9的算术平方根是( )A、±3 B、3 C、± D、5. 在实数-1.414, ,π, ,2+ ,3.212212221…,3.14中,无理数的个数是( )个.A、1 B、2 C、3 D、46. 已知 , , ,则 的值是( )A、24.72 B、53.25 C、11.47 D、114.77. 若点P(a,b)在第三象限,则点M(b-1,-a+1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 点P位于y轴左方,距y轴3个单位长,位于x轴上方,距x轴4个单位长,点P的坐标是( )A、 B、 C、 D、9. 若 , ,则 ( )A、 8 B、±8 C、±2 D、±8或±210. 如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
4. 9的算术平方根是( )A、±3 B、3 C、± D、5. 在实数-1.414, ,π, ,2+ ,3.212212221…,3.14中,无理数的个数是( )个.A、1 B、2 C、3 D、46. 已知 , , ,则 的值是( )A、24.72 B、53.25 C、11.47 D、114.77. 若点P(a,b)在第三象限,则点M(b-1,-a+1)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 点P位于y轴左方,距y轴3个单位长,位于x轴上方,距x轴4个单位长,点P的坐标是( )A、 B、 C、 D、9. 若 , ,则 ( )A、 8 B、±8 C、±2 D、±8或±210. 如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
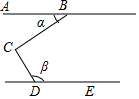 A、 B、 C、 D、11. 下列命题中,其中是真命题的是 ( )A、数2的平方根是 1 B、两条直线被第三条直线所截,同位角相等 C、点(x2 , 1)一定在第一象限 D、同角的补角相等12. 将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9,则表示实数2019的有序实数对是( )
A、 B、 C、 D、11. 下列命题中,其中是真命题的是 ( )A、数2的平方根是 1 B、两条直线被第三条直线所截,同位角相等 C、点(x2 , 1)一定在第一象限 D、同角的补角相等12. 将正整数按如图所示的规律排列下去,若有序实数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示实数9,则表示实数2019的有序实数对是( ) A、 B、(64,62) C、 D、
A、 B、(64,62) C、 D、二、填空题
-
13. 如果将电影票上“8排5号”简记为(8,5),那么“11排11号”可表示为 ;(5,6)表示的含义是 .14. 写出一个比-2 小的无理数 .15. 如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFG=65°,则∠2= .
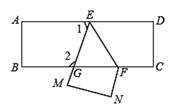 16. 命题“平行于同一条直线的两条直线互相平行”的题设是 , 结论是.17. 在平面直角坐标系中,点P(﹣1,2)向右平移3个单位长度再向上平移1个单位长度得到的点的坐标是 .18. 19.若a、b为实数,且满足 ,则a-b的立方根为.19. 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°),当∠ACE<90°且点E在直线AC的上方,使△ACD的一边与三角形ECB的某一边平行时,写出∠ACE的所有可能的值 .
16. 命题“平行于同一条直线的两条直线互相平行”的题设是 , 结论是.17. 在平面直角坐标系中,点P(﹣1,2)向右平移3个单位长度再向上平移1个单位长度得到的点的坐标是 .18. 19.若a、b为实数,且满足 ,则a-b的立方根为.19. 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°),当∠ACE<90°且点E在直线AC的上方,使△ACD的一边与三角形ECB的某一边平行时,写出∠ACE的所有可能的值 .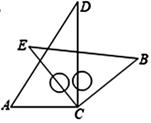
三、解答题:本大题共6个小题,满分74分.解答时请写出必要的演推过程.
-
20.(1)、计算: ;
(2)、求式中的x的值:4x2=25;21. 已知2a-1的算术平方根是3,3a+b-1的平方根是±4,c是 的整数部分,求a+2b-c的平方根.22. 在三角形中,每两条边所组成的角叫做三角形的内角,如图1,在三角形ABC中,∠A、∠B、∠ACB都是三角形ABC的内角.学习了平行线的性质后,我们可以用几何推理的方法证明“三角形的内角和等于180°”.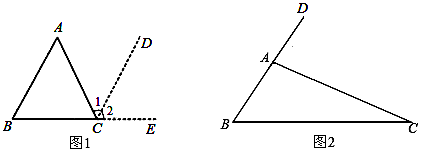
(1)、请根据给出的证明过程填空或填写理由;解:证明:如图1,延长BC,过点C作AB∥CD,
∵AB∥CD,
∴∠1=(),
∵AB∥CD,
∴∠2=(),
∵∠1+∠2+∠ACB=180°(平角的定义)
∴(等量代换)
即三角形的内角和等于180°.
(2)、如图2,若∠B=65°,∠C=20°,请根据题目的结论求出∠DAC的度数.
23. 如图,△ABC在直角坐标系中.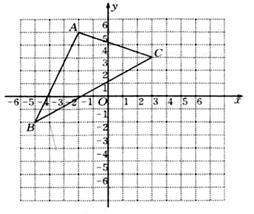 (1)、 请写出△ABC各点的坐标;(2)、 求出△ABC的面积;(3)、如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1 , 并写出点A1、B1、C1的坐标.24. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)、 请写出△ABC各点的坐标;(2)、 求出△ABC的面积;(3)、如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1 , 并写出点A1、B1、C1的坐标.24. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.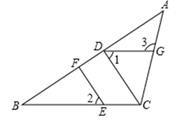
(1)、
试说明DG∥BC的理由;
(2)、如果∠B=54°,且∠ACD=35°,求∠3的度数25. 问题情境:在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.

(1)、如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;(2)、结论应用
如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于(用含α的式子表示).