广东省中山市2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2019-07-10 类型：期中考试

进入出卷网下载

一、单项选择题（共10个小题，每小题3分，满分30分）

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{8} \div 2 = \sqrt{2}$ B、 ${(2 \sqrt{2})}^{2} = 16$ C、 $2 \times \sqrt{\frac{3}{2}} = \sqrt{3}$ D、 $\sqrt{8} - \sqrt{2} = \sqrt{6}$

查看试题解析
3. 若△ABC的三边分别为5、12、13，则△ABC的面积是（）

A、30 B、40 C、50 D、60

查看试题解析
4. 下列各数中，与 $\sqrt{3}$ 的积为有理数的是（）

A、 $\sqrt{2}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{2}$ D、 $2 - \sqrt{3}$

查看试题解析
5. 在Rt△ABC中，∠C＝90°．如果BC＝3，AC＝5，那么AB＝（）

A、 $\sqrt{34}$ B、4 C、4或 $\sqrt{34}$ D、以上都不对

查看试题解析
6. 如图，下列哪组条件不能判定四边形ABCD是平行四边形（）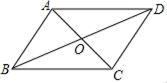

A、AB∥CD ， AB＝CD B、AB∥CD ， AD∥BC C、OA＝OC ， OB＝OD D、AB∥CD ， AD＝BC

查看试题解析
7. 如图，在∠MON的两边上分别截取OA、OB，使OA＝OB；分别以点A、B为圆心，OA长为半径作弧，两弧交于点C；连接AC、BC、AB、OC．若AB＝2cm，四边形OACB的面积为4cm2．则OC的长为（）cm

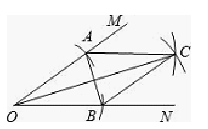A、2 B、3 C、4 D、5

查看试题解析
8. 如图，菱形ABCD的对角线相交于点O，若AC=8，BD=6，则菱形ABCD的周长是（）

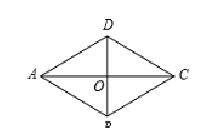A、32 B、24 C、20 D、40

查看试题解析
9. 矩形的对角线一定具有的性质是（）

A、互相垂直 B、互相垂直且相等 C、相等 D、互相垂直平分

查看试题解析
10. 如图，把一张正方形纸对折两次后，沿虚线剪下一角，展开后所得图形一定是（）

A、三角形 B、菱形 C、矩形 D、正方形

查看试题解析

二、填空题（共6个小题，每小题4分，满分24分）

11. 二次根式 $\sqrt{x - 3}$ 中字母x的取值范围是

查看试题解析
12. 定理“对角线互相平分的四边形是平行四边形”的逆命题是

查看试题解析
13. 如图，△ABC中，若∠ACB＝90°，∠B＝56°，D是AB的中点，则∠ACD＝°．

查看试题解析
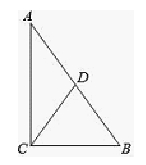14. 如图，四边形ABCD中，连接AC，AB∥DC，要使AD＝BC，需要添加的一个条件是．

查看试题解析
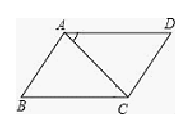15. 如图，正方形ABCD的周长为16 cm，则矩形EFCG的周长是 cm

查看试题解析
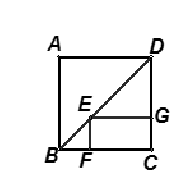16. 如图，已知等边三角形ABC边长为16，△ABC的三条中位线组成△A1B1C1，△A1B1C1的三条中位线组成△A2B2C2，依此进行下去得到△A4B4C4的周长为．

查看试题解析

三、解答题（一）（共3个小题，每小题6分，满分18分）

17. 化简： $\sqrt{45} + \sqrt{108} - 3 \sqrt{1 \frac{1}{3}} - \sqrt{125}$

查看试题解析
18. 如图，E、F分别为▱ABCD的边BC、AD上的点，且∠1=∠2．求证：四边形AECF是平行四边形．

查看试题解析
19. 已知矩形ABCD中，AD= $\sqrt{5} + \sqrt{3}$ ，AB= $\sqrt{5} - \sqrt{3}$ ，求这个矩形的的对角线AC的长及其面积

查看试题解析

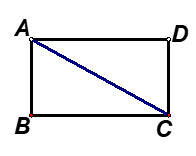
四、解答题（二）（共3个小题，每小题7分，满分21分）

20. 在甲村至乙村的公路有一块山地正在开发，现有一C处需要爆破．已知点C与公路上的停靠站A的距离为300米，与公路上的另一停靠站B的距离为400米，且CA⊥CB，如图所示．为了安全起见，爆破点C周围半径250米范围内不得进入，问在进行爆破时，公路AB段是否有危险而需要暂时封锁？请通过计算进行说明．

查看试题解析
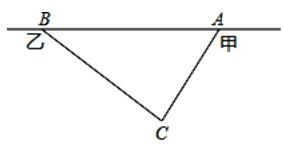21. 如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G，连接AG.

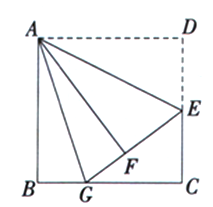(1)、求证：△ABG≌△AFG；

(2)、求BG的长.

查看试题解析
22. 如图，在△ABC中，AC＝9，AB＝12，BC＝15，P为BC边上一动点，PG⊥AC于点G，PH⊥AB于点H．

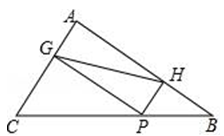(1)、求证：四边形AGPH是矩形；

(2)、在点P的运动过程中，GH的长度是否存在最小值？若存在，请求出最小值，若不存在，请说明理由．

查看试题解析

五、解答题（三）（共3个小题，每小题9分，满分27分）

23. 阅读下面材料，回答问题：

(1)、在化简 $\sqrt{5 - 2 \sqrt{6}}$ 的过程中，小张和小李的化简结果不同；
小张的化简如下： $\sqrt{5 - 2 \sqrt{6}}$ = $\sqrt{2 - 2 \sqrt{2 \times 3} + 3}$ = $\sqrt{{(\sqrt{2} - \sqrt{3})}^{2}}$ = $\sqrt{2} - \sqrt{3}$

小李的化简如下： $\sqrt{5 - 2 \sqrt{6}}$ = $\sqrt{2 - 2 \sqrt{3 \times 2} + 3}$ = $\sqrt{{(\sqrt{3} - \sqrt{2})}^{2}}$ = $\sqrt{3} - \sqrt{2}$

请判断谁的化简结果是正确的，谁的化简结果是错误的，并说明理由．

(2)、请你利用上面所学的方法化简：① $\sqrt{3 + 2 \sqrt{2}}$ ；② $\sqrt{6 - 2 \sqrt{5}}$ ．

查看试题解析
24. 在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．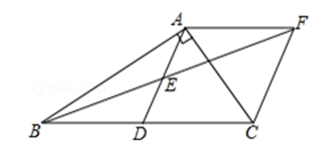

(1)、求证：△AEF≌△DEB；

(2)、判断：四边形ADCF是形，说明理由；

(3)、若AC=4，AB=5，求四边形ADCF的面积．

查看试题解析
25. 如图，在Rt△ABC中，∠B=90°，AC=12，∠A=60°．点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．

(1)、AB的长是．

(2)、在D、E的运动过程中，线段EF与AD的关系是否发生变化？若不变化，那么线段EF与AD是何关系，并给予证明；若变化，请说明理由．

(3)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．

查看试题解析