广东省深圳市盐田区2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期：2019-07-10 类型：期中考试
一、选择题：本题共12小题，每小题3分，共36分．
-
1. 20=（ ）A、1 B、 C、2 D、2. 0.00 000 13用科学记数法表示是（ ）A、1.3×10-5 B、1.3×10-6 C、0.13x10-5 D、0.13x10-63. 下列运算中，正确的是（ ）A、a2+2a2=3a4 B、b2·b3=b6 C、(x3)3=x6 D、y5÷y2=y34. 在同一平面内，（ ）A、不重合的两条直线要么平行要么相交 B、直角三角形的两锐角互补 C、两条直线平行，同旁内角相等 D、垂直于同一条直钱的两直线互相垂直5. 下列各组长度(单位：cm)的三条线段能组成三角形的是（ ）A、1，1，2 B、1，2，4 C、2，3，5 D、3，4，56. 三角形的重心是三条（ ）A、中线的交点 B、角平分线的交点 C、高线的交点 D、垂线的交点7. 若a-b=3，ab=1，则a2+b2=（ ）A、7 B、9 C、11 D、138. 佳佳从家坐车去书店，购书后骑单车回家，则她离家的距离S(m)与时间t(min)的关系的图象大致是（ ）A、
B、
C、
D、
9. 若(x+a)与(x+b)的乘积中不含x的一次项，则 的值是（ ）A、0 B、1 C、-1 D、±210. 已知弹簧的长度y(cm)与所挂物体的质量x(kg)之间有如下关系，则（ ）x(kg)
0
1
2
3
4
5
y(cm)
6
6.5
7
7.5
8
8
A、y随x的增大而增大 B、质量每增加1kg，度增加0.5cm C、不挂物体时，长度为6cm D、质量为6kg时，长度为8.cm11. 直线a∥b，一块含60°角的直角三角尺(∠A=60°)按如图所示放置．若∠1=45°，则∠2=（ ）
A、100° B、105° C、120° D、135°12. ∠A的两边与∠B的两边分别平行，∠A的度数比∠B的度数的2倍少30°，则∠A=（ ）A、30° B、60° C、60°或70° D、30°或110°二、填空题：本题共4小题，每小题3分，共12分．
-
13. 如图，AB∥CD，∠A=30°，∠E=90°，则∠C= 。
14. 某地的温度T(℃)与海拔高度h(km)之间的关系如下所示：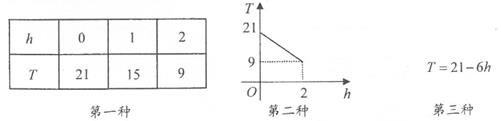
要算出海拔高度为6km时该地的温度，适宜用第种形式。
15. ∠A的余角是60°，则∠A的补角是。16. 佳佳用三根长度均为整数的木棒搭一个等腰三角形，其中一根木棒长为5，则另两根木棒最短可以为 ．三、解答题：本题共7小题，共52分．
-
17.(1)、计算：(2x+y)(x-y)(2)、用乘法公式计算：98×10218. 先化简，再求值：[（2a+b）2-(2a+b)(2a-b)]-1,其中a=-1，b=1。19. 如图，AB∥CD，点E是射线CD上一点．
(1)、在射线AB上取点F，利用尺规作图，使∠FED=∠C(用黑色水笔描粗作图痕迹，不要求写作法)；(2)、∠AFE与∠C相等吗?说明理由．20. 如图，∠ABC=∠ADE，∠1+∠2=180°， ∠BEC=80°，将求∠CGF的过程填写完整．解：因为∠ABC=∠ADE，
所以BC∥①(②)．
所以∠2=③
又因为∠1+∠2=180°，
所以∠1+④=180°．
所以BE∥GF(⑤)．
所以∠CGF=⑥(⑦)．
因为CEB=80°，
所以∠CGF=⑧ ．
21. 出租车车费计价标准为：3km以内（含3km）8元，超出3km的部分1.6元/km．(1)、佳佳乘出租车行驶4km，应付车费多少元?(2)、佳佳付车费16元，那么出租车行驶了多少km?(3)、直接写出车费y(元)与行驶路程x(km)之间的关系式．(其中x≥3)·22. 水池有若干个进水口与出水口，每个口进出水的速度如图1、图2所示，只开1个进水口持续15小时可将水池注满．
(1)、某段时间内蓄水量V(m3)与时间t(h)的关系如图3所示，0～3时只开2个进水口，3~b时只开1个进水口与1个出水口，9~c只开1个出水口，求证：a=b+c．(2)、若同时开2个出水口与1个进水口，多久可将满池的水排完?23.(1)、求证：三角形三个内角的和等于180°．
(2)、阅读材料并回答问题：如图，把△ABC的一边BC延长，得到∠ACD．像这样，三角形的一边与另一边的延长线组成的角，叫做三角形的“外角”，在每个顶点处取这个三角形的一个外角，它们的和叫做这个三角形的“外角和”．
补全图形并求△ABC的“外角和”．
