吉林省长春市二道区2018-2019学年九年级上学期数学第一次月考试卷

试卷更新日期：2019-07-10 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列二次根式中能与2 $\sqrt{3}$ 合并的是（）

A、 $\sqrt{8}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{18}$ D、 $\sqrt{9}$

查看试题解析
2. 已知 $\frac{a}{2} = \frac{b}{3}$ （a≠0，b≠0），下列变形错误的是（）

A、2a=3b B、 $\frac{a}{b}$ = $\frac{2}{3}$ C、3a=2b D、 $\frac{b}{a}$ = $\frac{3}{2}$

查看试题解析
3. 在Rt△ABC中，∠C=90°，各边都扩大2倍，则锐角A的正弦值（）

A、扩大2倍 B、缩小 $\frac{1}{2}$ C、不变 D、无法确定

查看试题解析
4. 如图，A，B，C是小正方形的顶点，且每个小正方形的边长为1，则tan∠BAC的值为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{\sqrt{3}}{3}$ D、 $\sqrt{3}$

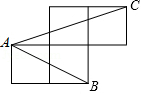查看试题解析
5. 若顺次连结四边形四条边的中点，所得的四边形是菱形，则原四边形一定是（）

A、平行四边形 B、矩形 C、对角线相等的四边形 D、对角线互相垂直的四边形

查看试题解析

二、填空题

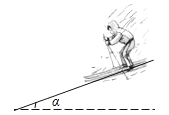
6. 若式子 $\sqrt{5 - x}$ 有意义，则x的取值范围是．

查看试题解析
7. 以m=为反例，可以证明命题“关于x的一元二次方程x²+x+m=0必有实数根”是错误的命题（写出一个m值即可）．

查看试题解析
8. 如图，一人乘雪橇沿坡角为α的斜坡笔直滑行了82米，那么他下降的高度为米（用含α的式子表示）．

查看试题解析
9. 如图，△DEF是由△ABC经过位似变换得到的，点O是位似中心， $\frac{OD}{DA}$ = $\frac{2}{3}$ ，则△DEF与△ABC的面积比是．

查看试题解析
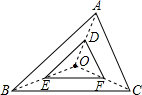10. 某玩具商店出售一种“小猪佩奇”玩具，平均每天可销售50个，每个盈利36元，为了尽快减少库存，商场决定采取适当的降价措施，调查发现，若每个玩具降价1元，平均每天可多售出5个，商店要想平均每天销售这种玩具盈利2400元，则每个玩具应降价多少元？设每个玩具应降价x元，可列方程为．

查看试题解析
11. 如图，已知正方形DEFG的顶点D、E在△ABC的边BC上，顶点G、F分别在边AB、AC上．如果BC=4，△ABC的面积是6，那么这个正方形的边长是．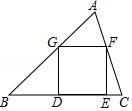

查看试题解析

三、解答题

12. 计算： $\sqrt{\frac{1}{2}}$ × $\sqrt{48}$ ﹣（ $\sqrt{\frac{1}{8}}$ + $\sqrt{6}$ ）+2sin45°．

查看试题解析
13. 对于实数a、b，定义运算※如下，a※b=a²﹣ab，例如，5※3=5²﹣5×3=10．若（x+1）※（3x﹣2）=0，求x的值．

查看试题解析
14. 如图，图①、图②、图③均为4×2的正方形网格，△ABC的顶点均在格点上．按要求在图②、图③中各画一个顶点在格点上的三角形．
要求：

⑴所画的两个三角形都与△ABC相似但都不与△ABC全等．

⑵图②和图③中新画的三角形不全等．

查看试题解析
15. 如图，某餐厅的餐桌桌面是一个面积为0.84m²的矩形，桌面装有两个表面为相同正方形的电磁炉，两个电磁炉之间及与四周的距离均为0.2m，求电磁炉表面的边长．

查看试题解析
16. 在△ABC中，AB=6，AC=8，D、E分别在AB、AC上，连接DE，设BD=x（0＜x＜6），CE=y（0＜y＜8）．

(1)、当x=2，y=5时，求证：△AED∽△ABC；

(2)、若△ADE和△ABC相似，求y与x的函数表达式．

查看试题解析
17. 图1是一辆吊车的实物图，图2是其工作示意图，AC是可以伸缩的起重臂，其转动点A离地面BD的高度AH为3.4m．当起重臂AC长度为9m，张角∠HAC为118°时，求操作平台C离地面的高度（结果保留小数点后一位：参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）

查看试题解析
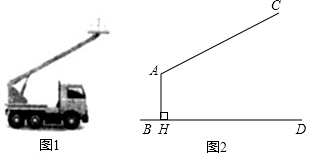18. 阅读下面的文字，解答问题：大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $\sqrt{2}$ ﹣1来表示 $\sqrt{2}$ 的小数部分，事实上，小明的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是 $\sqrt{2}$ 的小数部分，又例如：∵2²＜（ $\sqrt{7}$ ）²＜3² ，即2＜ $\sqrt{7}$ ＜3，∴ $\sqrt{7}$ 的整数部分为2，小数部分为（ $\sqrt{7}$ ﹣2）．
请解答：

(1)、 $\sqrt{11}$ 的整数部分是，小数部分是．

(2)、如果 $\sqrt{5}$ 的小数部分为a， $\sqrt{41}$ 的整数部分为b，求a+b﹣ $\sqrt{5}$ 的值．

(3)、已知x是3+ $\sqrt{5}$ 的整数部分，y是其小数部分，直接写出x﹣y的值．

查看试题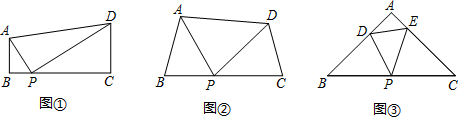解析
19. 如图

(1)、感知：如图①，在四边形ABCD中，AB∥CD，∠B=90°，点P在BC边上，当∠APD=90°时，可知△ABP∽△PCD．（不要求证明）

(2)、探究：如图②，在四边形ABCD中，点P在BC边上，当∠B=∠C=∠APD时，求证：△ABP∽△PCD．

(3)、拓展：如图③，在△ABC中，点P是边BC的中点，点D、E分别在边AB、AC上．若∠B=∠C=∠DPE=45°，BC=6 $\sqrt{2}$ ，CE=4，则DE的长为．

查看试题解析
20. 我们知道，解一元二次方程，可以把它转化为两个一元一次方程来解，其实用“转化”的数学思想，我们还可以解一些新的方程，例如一元三次方程x³+x²﹣2x=0，可以通过因式分解把它转化为x（x²+x﹣2）=0，解方程x=0和x²+x﹣2=0，可得方程x³+x²﹣2x=0的解．

(1)、方程x³+x²﹣2x=0的解是x₁=0，x₂= ， x₃= ．

(2)、用“转化”思想求方程 $\sqrt{2 x + 3}$ =x的解．

(3)、如图，已知矩形草坪ABCD的长AD=14m，宽AB=12m，小华把一根长为28m的绳子的一端固定在点B处，沿草坪边沿BA、AD走到点P处，把长绳PB段拉直并固定在点P处，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C处，求AP的长．

查看试题解析
21. 如图，在Rt△ABC中，∠ACB=90°，AC=3，AB=5．点P从点A出发，以每秒5个单位长度的速度沿AC方向运动，过点P作PQ⊥AB于点Q，当点Q和点B重合时，点P停止运动，以AP和AQ为边作▱APHQ．设点P的运动时间为t秒（t＞0）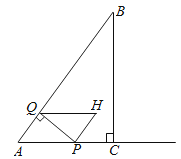

(1)、线段PQ的长为．（用含t的代数式表示）

(2)、当点H落在边BC上时，求t的值．

(3)、当▱APHQ与△ABC的重叠部分图形为四边形时，设四边形的面积为S，求S与t之间的函数关系式．

(4)、过点C作直线CD⊥AB于点D，当直线CD将▱APHQ分成两部分图形的面积比为1：7时，直接写出t的值．

查看试题解析