山西省太原市2018-2019学年中考数学一模考试试卷
试卷更新日期:2019-07-09 类型:中考模拟
一、单选题
-
1. 计算“-2019+2018”的结果是( )A、-1 B、1 C、-4037 D、40372. 下列各项调查中,最适合用全面调查(普查)的是( )A、了解国内外观众对电影《流浪地球》的观影感受 B、了解太原市九年级学生每日睡眠时长 C、“长征-3B火箭”发射前,检查其各零部件的合格情况 D、检测一批新出厂的手机的使用寿命3. 如图,含45°角的三角板的直角顶点A在直线a上,顶点C在直线b上.若a∥b , ∠1=60°,则∠2的度数为( )
 A、95° B、105° C、110° D、115°4. 2018年我省着力提高能源供给体系质量,推动煤炭产业走“减、优、绿”的路子,全省煤炭先进产能占比达到57%,建成“两交一直”特高压输电通道,外送能力达到3830万千瓦.数据“3830万千瓦”用科学记数法表示为( )A、3830´104千瓦 B、383´105千瓦 C、0.383´108千瓦 D、3.83´107千瓦5. 由木炭,铅笔,钢笔等,以线条来画出物象明暗的单色面,称作素描.如图是素描初学者常用的一种石膏几何体,该几何体的形状可以看成是用一个平面截圆柱体得到的,它的俯视图是( )
A、95° B、105° C、110° D、115°4. 2018年我省着力提高能源供给体系质量,推动煤炭产业走“减、优、绿”的路子,全省煤炭先进产能占比达到57%,建成“两交一直”特高压输电通道,外送能力达到3830万千瓦.数据“3830万千瓦”用科学记数法表示为( )A、3830´104千瓦 B、383´105千瓦 C、0.383´108千瓦 D、3.83´107千瓦5. 由木炭,铅笔,钢笔等,以线条来画出物象明暗的单色面,称作素描.如图是素描初学者常用的一种石膏几何体,该几何体的形状可以看成是用一个平面截圆柱体得到的,它的俯视图是( ) A、
A、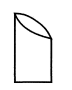 B、
B、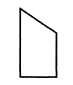 C、
C、 D、
D、 6. 下列运算正确的是( )A、a2×a3=a6 B、 =±5 C、2 D、(a+1)(a-2)=a2-27. 如图,过⊙O上一点A作⊙O的切线,交直径BC的延长线与点D,连接AB,若∠B=25°,则∠D的度数为( )
6. 下列运算正确的是( )A、a2×a3=a6 B、 =±5 C、2 D、(a+1)(a-2)=a2-27. 如图,过⊙O上一点A作⊙O的切线,交直径BC的延长线与点D,连接AB,若∠B=25°,则∠D的度数为( ) A、25° B、40° C、45° D、50°8. 计算 的结果为( )A、 B、 C、a-2 D、a+29. 如图,ΔABC中,∠BAC=90°,AB=AC,延长CA至点D,使AD=AC,点E是BC的中点,连接DE交AB于点F,则AF:FB的值为( )
A、25° B、40° C、45° D、50°8. 计算 的结果为( )A、 B、 C、a-2 D、a+29. 如图,ΔABC中,∠BAC=90°,AB=AC,延长CA至点D,使AD=AC,点E是BC的中点,连接DE交AB于点F,则AF:FB的值为( )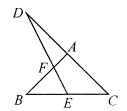 A、 B、 C、 D、10. 德国数学家高斯在大学二年级时得出了正十七边形是尺规作图法,并给出了可用尺规作图的正多边形的条件.下面是高斯正十七边形作法的一部分:“如图,已知AB是圆O的直径,分别以A,B为圆心、AB长为半径作弧,两弧交于点C,D两点…”.若AB长为2,则图中弧CAD的长为( )
A、 B、 C、 D、10. 德国数学家高斯在大学二年级时得出了正十七边形是尺规作图法,并给出了可用尺规作图的正多边形的条件.下面是高斯正十七边形作法的一部分:“如图,已知AB是圆O的直径,分别以A,B为圆心、AB长为半径作弧,两弧交于点C,D两点…”.若AB长为2,则图中弧CAD的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
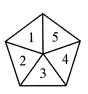
11. 如图是一个正五边形形状的飞镖游戏板,被分成大小相等的五份,分别标有数字1,2,3,4,5,向游戏板随机投掷一次飞镖(当飞镖投掷在分割线上时,则重投一次),击中的区域中所标数字恰好为奇数的概率是.
 12. 如图,△ABC沿射线AC的方向平移,得到△CDE.若AE=6,则B,D两点的距离为.
12. 如图,△ABC沿射线AC的方向平移,得到△CDE.若AE=6,则B,D两点的距离为.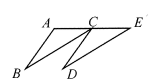 13. 如图是一组有规律的图案,它们由半径相同的圆形组成,依此规律,第n个图案中有个圆形(用含有n的代数式表示).
13. 如图是一组有规律的图案,它们由半径相同的圆形组成,依此规律,第n个图案中有个圆形(用含有n的代数式表示).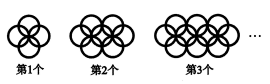 14. 从2019年3月26日开始,由支付宝给信用卡还款将开始收取服务费.据规定,每月还款2000元及以内不收费,超过2000元的部分将按照0.1%的比例来收取服务费.按此规定,小李下期通过支付宝给信用卡还款将支付5元的服务费.若小李此次还款总额为x元,则x满足的方程为.15. 如图,在矩形ABCD中,点E,F分别在BC,CD边上,且CE=3,CF=4.若△AEF是等边三角形,则AB的长为.
14. 从2019年3月26日开始,由支付宝给信用卡还款将开始收取服务费.据规定,每月还款2000元及以内不收费,超过2000元的部分将按照0.1%的比例来收取服务费.按此规定,小李下期通过支付宝给信用卡还款将支付5元的服务费.若小李此次还款总额为x元,则x满足的方程为.15. 如图,在矩形ABCD中,点E,F分别在BC,CD边上,且CE=3,CF=4.若△AEF是等边三角形,则AB的长为.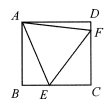
三、解答题
-
16.(1)、计算: ;(2)、解不等式组: 并将其解集表示在如图所示的数轴上.
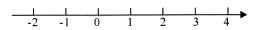 17. 如图,点E,F分别在平行四边形ABCD的边BA,DC的延长线上,连接EF,交对角线BD于点O,已知OE=OF.
17. 如图,点E,F分别在平行四边形ABCD的边BA,DC的延长线上,连接EF,交对角线BD于点O,已知OE=OF.
求证:四边形EBFD是平行四边形.
18. 平面直角坐标系中,反比例函数y= 的图象与一次函数y=– x−2的图象交于A(–6,m),B(n , –3)两点,点C与点B关于原点对称,过点C作x轴的垂线交直线AB于点D . (1)、求反比例函数y= 的表达式及点C的坐标;(2)、求△ACD的面积.19. 学校组织首届“数学文化节”活动,旨在引导同学们感受数学魅力、提升数学素养。活动中,七年级全体同学参加了“趣味数学知识竞赛”。
(1)、求反比例函数y= 的表达式及点C的坐标;(2)、求△ACD的面积.19. 学校组织首届“数学文化节”活动,旨在引导同学们感受数学魅力、提升数学素养。活动中,七年级全体同学参加了“趣味数学知识竞赛”。收集数据:现随机抽取七年级中40名同学“趣味数学知识竞赛”的成绩,如下(单位:分):
7585758075758570759075808070758085808095
9575908070809585758580807080758080557060
整理分析:小彬按照如下表格整理了这组数据,并绘制了如下的频数直方图。
 (1)、请将图表中空缺的部分补充完整,并说明这40名同学“趣味数学知识竞赛”的成绩分布情况(写出一条即可);(2)、这40名同学的“趣味数学知识竞赛”成绩的中位数是分;
(1)、请将图表中空缺的部分补充完整,并说明这40名同学“趣味数学知识竞赛”的成绩分布情况(写出一条即可);(2)、这40名同学的“趣味数学知识竞赛”成绩的中位数是分;问题解决:
(3)、“数学文化节”组委会决定,给“趣味数学知识竞赛”成绩在90分及90分以上的同学授予“数学之星”称号。根据上面统计结果估计该校七年级560人中,约有多少人将获得“数学之星”称号?(4)、“数学文化节”中,获得“数学之星”称号的小颖得到了A,B,C,D四枚纪念章(除头像外完全相同)。如图所示,四枚纪念章上分别印有四位数学家的头像。她将纪念章背面朝上放在桌面上,然后从中随机选取两枚送给妹妹。求小颖送给妹妹的两枚纪念章中恰好有一枚印有华罗庚头像的概率。(提示:答题时可用序号A,B,C,D表示相应的纪念章) 20. S56太原—古交高速公路全长23.4千米,是山西省高速公路网规划的太原区域环的重要组成部分。施工中,工人们穿越煤层区、采空区等不良地质带,克服了多种危险因素,使得天堑变通途。这段公路建有2座隧道(分别是西山特长隧道和西山2号隧道),它们总长达15千米。其中,特长隧道的长度比西山2号隧道长度的9倍还多1千米。
20. S56太原—古交高速公路全长23.4千米,是山西省高速公路网规划的太原区域环的重要组成部分。施工中,工人们穿越煤层区、采空区等不良地质带,克服了多种危险因素,使得天堑变通途。这段公路建有2座隧道(分别是西山特长隧道和西山2号隧道),它们总长达15千米。其中,特长隧道的长度比西山2号隧道长度的9倍还多1千米。 (1)、求西山特长隧道与西山2号隧道的长度;(2)、某日,小王驾车经S56太原——古交高速从古交到太原。他7:28进入高速,计划出高速口的时间不超过7:50.按照他的驾车习惯,在隧道内的平均速度为60千米/时,则他在非隧道路段的平均车速至少为多少千米/时?21. 清代诗人高鼎的诗句“儿童散学归来早,忙趁东风放纸鸢”描绘出一幅充满生机的春天景象。小明制作了一个风筝,如图1所示,AB是风筝的主轴,在主轴AB上的D、E两处分别固定一根系绳,这两根系绳在C点处打结并与风筝线连接。如图2,根据试飞,将系绳拉直后,当∠CDE=75°,∠CED=60°时,放飞效果佳。已知D、E两点之间的距离为20cm,求两根系绳CD、CE的长。(结果保留整数,不计打结长度。参考数据: )
(1)、求西山特长隧道与西山2号隧道的长度;(2)、某日,小王驾车经S56太原——古交高速从古交到太原。他7:28进入高速,计划出高速口的时间不超过7:50.按照他的驾车习惯,在隧道内的平均速度为60千米/时,则他在非隧道路段的平均车速至少为多少千米/时?21. 清代诗人高鼎的诗句“儿童散学归来早,忙趁东风放纸鸢”描绘出一幅充满生机的春天景象。小明制作了一个风筝,如图1所示,AB是风筝的主轴,在主轴AB上的D、E两处分别固定一根系绳,这两根系绳在C点处打结并与风筝线连接。如图2,根据试飞,将系绳拉直后,当∠CDE=75°,∠CED=60°时,放飞效果佳。已知D、E两点之间的距离为20cm,求两根系绳CD、CE的长。(结果保留整数,不计打结长度。参考数据: )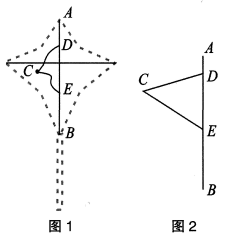 22. 综合与实践
22. 综合与实践数学活动:在综合与实践活动课上,老师让同学们以“三角形纸片的折叠、旋转”为主题开展数学活动,探究线段长度的有关问题.
动手操作:如图1,在直角三角形纸片ABC中,∠BAC=90°,AB=6,AC=8.将三角形纸片ABC进行以下操作:
第一步:折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE;
第二步:将△ABC沿折痕DE展开,然后将△DEC绕点D逆时针方向旋转得到△DFG,点E,C的对应点分别是点F,G,射线GF与边AC交于点M(点M不与点A重合),与边AB交于点N,线段DG与边AC交于点P.
数学思考:
 (1)、求DC的长;(2)、在△DEC绕点D旋转的过程中,试判断MF与ME的数量关系,并证明你的结论;
(1)、求DC的长;(2)、在△DEC绕点D旋转的过程中,试判断MF与ME的数量关系,并证明你的结论;问题解决:
(3)、在△DEC绕点D旋转的过程中,探究下列问题:①如图2,当GF∥BC时,求AM的长;
②如图3,当GF经过点B时,AM的长为
③当△DEC绕点D旋转至DE平分∠FDG的位置时,试在图4中作出此时的△DFG和射线GF,并直接写出AM的长(要求:尺规作图,不写作法,保留作图痕迹,标记出所有相应的字母)
23. 综合与研究如图,抛物线y=-x2-2x+3与x轴交于A、B两点(A在B的左侧),与y轴交于点C.点D(m,0)为线段OA上一个动点(与点A,O不重合),过点D作x轴的垂线与线段AC交于点P,与抛物线交于点Q,连接BP,与y轴交于点E.
 (1)、求A,B,C三点的坐标;(2)、当点D是OA的中点时,求线段PQ的长;(3)、在点D运动的过程中,探究下列问题:
(1)、求A,B,C三点的坐标;(2)、当点D是OA的中点时,求线段PQ的长;(3)、在点D运动的过程中,探究下列问题:①是否存在一点D,使得PQ+ PC取得最大值?若存在,求此时m的值;若不存在,请说明理由;
②连接CQ,当线段PE=CQ时,直接写出m的值.