山西省大同市2018-2019学年中考数学二模考试试卷
试卷更新日期:2019-07-09 类型:中考模拟
一、单选题
-
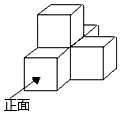
1. 下列结果为2的是( )A、﹣(+2) B、 C、|﹣2| D、﹣|﹣2|2. 如图是由五个相同的小正方体组成的立体图形,从上面看到的图形是( )
 A、
A、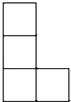 B、
B、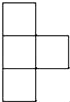 C、
C、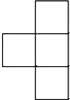 D、
D、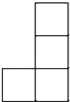 3. 下列运算正确的是( )A、﹣(a3)2=a5 B、a2+a2=a4 C、 =4 D、| ﹣2|= ﹣24. 如图,把三角板的直角顶点放在直尺的一边上,若∠1=27°,则∠2的度数是( )
3. 下列运算正确的是( )A、﹣(a3)2=a5 B、a2+a2=a4 C、 =4 D、| ﹣2|= ﹣24. 如图,把三角板的直角顶点放在直尺的一边上,若∠1=27°,则∠2的度数是( )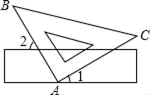 A、53° B、63° C、73° D、27°5. 不等式组 的解集在数轴上表示正确的是( )A、
A、53° B、63° C、73° D、27°5. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、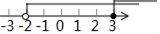 C、
C、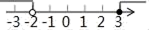 D、
D、 6. “山西八分钟,惊艳全世界”.2019年2月25日下午,在外交部蓝厅隆重举行山西全球推介活动.山西经济结构从“一煤独大”向多元支撑转变,三年累计退出煤炭过剩产能8800余万吨,煤层气产量突破56亿立方米.数据56亿用科学记数法可表示为( )
6. “山西八分钟,惊艳全世界”.2019年2月25日下午,在外交部蓝厅隆重举行山西全球推介活动.山西经济结构从“一煤独大”向多元支撑转变,三年累计退出煤炭过剩产能8800余万吨,煤层气产量突破56亿立方米.数据56亿用科学记数法可表示为( ) A、56×108 B、5.6×108 C、5.6×109 D、0.56×10107. 将抛物线y=x2﹣x+1先向左平移2个单位长度,再向上平移3个单位长度,则所得抛物线的表达式为( )A、y=x2+3x+6 B、y=x2+3x C、y=x2﹣5x+10 D、y=x2﹣5x+48. 《九章算术》是中国传统数学最重要的著作之一,其中记载:“今有共买物人出八,盈三;人出七,不足四问人数、物价各几何?”译文:“几个人去购买物品,如果每人出8钱,则剩余3钱;如果每人出7钱,则差4钱问有多少人,物品的价格是多少”?设有m人,物品价格是n钱,下列四个等式:①8m+3=7m﹣4;② = ;③ = ;④8m﹣3=7m+4,其中正确的是( )
A、56×108 B、5.6×108 C、5.6×109 D、0.56×10107. 将抛物线y=x2﹣x+1先向左平移2个单位长度,再向上平移3个单位长度,则所得抛物线的表达式为( )A、y=x2+3x+6 B、y=x2+3x C、y=x2﹣5x+10 D、y=x2﹣5x+48. 《九章算术》是中国传统数学最重要的著作之一,其中记载:“今有共买物人出八,盈三;人出七,不足四问人数、物价各几何?”译文:“几个人去购买物品,如果每人出8钱,则剩余3钱;如果每人出7钱,则差4钱问有多少人,物品的价格是多少”?设有m人,物品价格是n钱,下列四个等式:①8m+3=7m﹣4;② = ;③ = ;④8m﹣3=7m+4,其中正确的是( ) A、①② B、②④ C、②③ D、③④9. 寒假期间,小刚组织同学一起去看科幻电影《流浪地球》,票价每张45元,20张以上(不含20张)打八折,他们一共花了900元,则他们买到的电影票的张数是( )A、20 B、22 C、25 D、20或2510. 如图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC,△ABC的三边所围成的区域面积记为S1 , 黑色部分面积记为S2 , 其余部分面积记为S3 , 则( )
A、①② B、②④ C、②③ D、③④9. 寒假期间,小刚组织同学一起去看科幻电影《流浪地球》,票价每张45元,20张以上(不含20张)打八折,他们一共花了900元,则他们买到的电影票的张数是( )A、20 B、22 C、25 D、20或2510. 如图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC,△ABC的三边所围成的区域面积记为S1 , 黑色部分面积记为S2 , 其余部分面积记为S3 , 则( ) A、S1=S2 B、S1=S3 C、S2=S3 D、S1=S2+S3
A、S1=S2 B、S1=S3 C、S2=S3 D、S1=S2+S3二、填空题
-
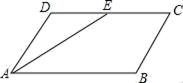
11. 计算:(a+b)(2a﹣2b)= .12. 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为 .
 13. 若反比例函数 的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是 .
13. 若反比例函数 的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是 .
14. 某校园餐厅把WIF密码做成了数学题,小亮在餐厅就餐时,思索了一会,输入密码,顺利地连接到了学子餐厅的网络,那么他输入的密码是 . 15. 如图,在正方形ABCD中,F是AD的中点,E是CD上一点,∠FBE=45°,则tan∠FEB的值是 .
15. 如图,在正方形ABCD中,F是AD的中点,E是CD上一点,∠FBE=45°,则tan∠FEB的值是 .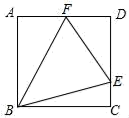
三、解答题
-
16. 计算:(1)、(2)、17. 如图,一次函数y1=kx+b(k≠0)和反比例函数 的图象相交于点A(﹣4,2),B(n,﹣4)
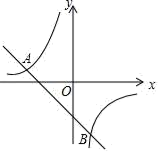 (1)、求一次函数和反比例函数的表达式;(2)、观察图象,直接写出不等式y1<y2的解集.18. 如图,在直角坐标系xOy中,O为坐标原点,直线AB分别与y轴,x轴交于A(0,4),B(3,0)两点.
(1)、求一次函数和反比例函数的表达式;(2)、观察图象,直接写出不等式y1<y2的解集.18. 如图,在直角坐标系xOy中,O为坐标原点,直线AB分别与y轴,x轴交于A(0,4),B(3,0)两点.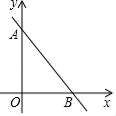 (1)、尺规作图:在x轴上求作一点C,使△ABC是以∠C为顶角的等腰三角形,并在图中标明相应字母.(保留作图痕迹,不写作法)(2)、在(1)的条件下,求点C的坐标.19. 目前“微信”以其颠覆性的创新,赢得了数亿人的支持,为了调查某中学学生在周日上“微信”的时间,随机对100名男生和100名女生进行了问卷调查,得到了如下的统计结果
(1)、尺规作图:在x轴上求作一点C,使△ABC是以∠C为顶角的等腰三角形,并在图中标明相应字母.(保留作图痕迹,不写作法)(2)、在(1)的条件下,求点C的坐标.19. 目前“微信”以其颠覆性的创新,赢得了数亿人的支持,为了调查某中学学生在周日上“微信”的时间,随机对100名男生和100名女生进行了问卷调查,得到了如下的统计结果表1:男生上“微信时间的频数分布表
上网时间(分钟)
30≤x<40
40≤x<50
50≤x<60
60≤x<70
70≤x<80
人数
5
25
30
25
15
表2:女生上“微信”时间的频数分布表
上网时间(分钟)
30≤x<40
40≤x<50
50≤x<60
60≤x<70
70≤x<80
人数
10
20
40
20
10
请结合图表完成下列各题
(1)、完成表3:表3
上“微信”时间少于60分钟
上“微信”时间不少于60分钟
男生人数
女生人数
(2)、若该中学共有女生750人,请估计其中上“微信”时间不少于60分钟的人数;(3)、从表3的男生中抽取5人(其中3人上“微信”时间少于60分钟,2人上“微信”时间不少于60分钟),再从抽取的5人中任取2人,请用列表或画树状图的方法求出至少有一人上“微信”时间不少于60分钟的概率.20. 大张高铁是连接晋北地区与京津冀地区的重要交通枢纽,也是大同市的“一号工程”,大张高铁预计于今年9月进行联调联试,并计划年底开通大张高铁开通后,从大同至北京的列车运行时间将比普通列车缩短4 小时,已知大同到北京全程约350千米,高铁列车的速度是普通列车速度的3.6倍,求从大同乘坐高铁到北京需要多长时间?21. 阅读下列材料,并完成相应的任务.托勒密定理:
托勒密(Ptolemy)(公元90年~公元168年),希腊著名的天文学家,他的要著作《天文学大成》被后人称为“伟大的数学书”,托勒密有时把它叫作《数学文集》,托勒密从书中摘出并加以完善,得到了著名的托勒密(Ptolemy)定理.

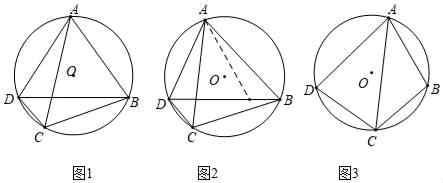
托勒密定理:
圆内接四边形中,两条对角线的乘积等于两组对边乘积之和.
已知:如图1,四边形ABCD内接于⊙O,
求证:AB•CD+BC•AD=AC•BD
下面是该结论的证明过程:
证明:如图2,作∠BAE=∠CAD,交BD于点E.
∵
∴∠ABE=∠ACD
∴△ABE∽△ACD
∴
∴AB•CD=AC•BE
∵
∴∠ACB=∠ADE(依据1)
∵∠BAE=∠CAD
∴∠BAE+∠EAC=∠CAD+∠EAC
即∠BAC=∠EAD
∴△ABC∽△AED(依据2)
∴AD•BC=AC•ED
∴AB•CD+AD•BC=AC•(BE+ED)
∴AB•CD+AD•BC=AC•BD
任务:
(1)、上述证明过程中的“依据1”、“依据2”分别是指什么?(2)、当圆内接四边形ABCD是矩形时,托勒密定理就是我们非常熟知的一个定理: .(请写出)
(3)、如图3,四边形ABCD内接于⊙O,AB=3,AD=5,∠BAD=60°,点C为 的中点,求AC的长.22. 综合与实践问题情境:如图1,在数学活动课上,老师让同学们画了等腰Rt△ABC和等腰Rt△ADE,并连接CE,BD.
 (1)、操作发现:当等腰Rt△ADE绕点A旋转,如图2,勤奋小组发现了:
(1)、操作发现:当等腰Rt△ADE绕点A旋转,如图2,勤奋小组发现了:①线段CE与线段BD之间的数量关系是 .
②直线CE与直线BD之间的位置关系是 .
(2)、类比思考:智慧小组在此基础上进行了深入思考,如图3,若△ABC与△ADE都为直角三角形,∠BAC=∠DAE=90°,且AC=2AB,AE=2AD,请你写出CE与BD的数量关系和位置关系,并加以证明.(3)、拓展应用:创新小组在(2)的基础上,又作了进一步拓展研究,当点E在直线AB上方时,若DE∥AB,且AB= ,AD=1,其他条件不变,试求出线段CE的长.(直接写出结论)23. 综合与探究如图,已知抛物线y=ax2﹣3x+c与y轴交于点A(0,﹣4),与x轴交于点B(4,0),点P是线段AB下方抛物线上的一个动点.
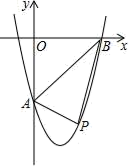 (1)、求这条抛物线的表达式及其顶点的坐标;(2)、当点P移动到抛物线的什么位置时,∠PAB=90°求出此时点P的坐标;(3)、当点P从点A出发,沿线段AB下方的抛物线向终点B移动,在移动中,设点P的横坐标为t,△PAB的面积为S,求S关于t的函数表达式,并求t为何值时S有最大值,最大值是多少?
(1)、求这条抛物线的表达式及其顶点的坐标;(2)、当点P移动到抛物线的什么位置时,∠PAB=90°求出此时点P的坐标;(3)、当点P从点A出发,沿线段AB下方的抛物线向终点B移动,在移动中,设点P的横坐标为t,△PAB的面积为S,求S关于t的函数表达式,并求t为何值时S有最大值,最大值是多少?