福建省南平市八校联考2018-2019学年中考数学模拟考试试卷

试卷更新日期：2019-07-09 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣8的相反数是（）

A、﹣8 B、 $\frac{1}{8}$ C、8 D、﹣ $\frac{1}{8}$

查看试题解析
2. 下列图案中既是轴对称又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 我国倡导的“一带一路”地区覆盖的总人口为4400000000人，这个数用科学记数法表示为（）

A、44×10⁸ B、4.4×10⁸ C、4.4×10⁹ D、44×10¹⁰

查看试题解析
4. 如图，⊙O是△ABC的外接圆，∠OCB＝40°，则∠A的大小为（）

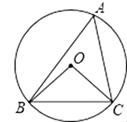A、40° B、50° C、80° D、100°

查看试题解析
5. 中国古代数学著作《九章算术》在世界数学史上首次正式引入负数，如果收入100元记作+100元，那么﹣90元表示（）

A、支出10元 B、收入10元 C、支出90元 D、收入90元

查看试题解析
6. 小明在计算一组样本数据的方差时，列出的公式如下：s²＝ $\frac{1}{n} [{(7 - \bar{x})}^{2} + {(8 - \bar{x})}^{2} + {(8 - \bar{x})}^{2} + {(8 - \bar{x})}^{2} + {(9 - \bar{x})}^{2}]$ ，根据公式信息，下列说法错误的是（）

A、样本容量是5 B、样本平均数是8 C、样本众数是8 D、样本方差是0

查看试题解析
7. 如图，在△ABC中，D，E分别在边AC与AB上，DE∥BC，BD、CE相交于点O， $\frac{E O}{O C} = \frac{1}{3}$ ，AE＝1，则EB的长为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，在Rt△ABC中，AC＝BC＝2，将△ABC绕点A逆时针旋转60°，连接BD ，则图中阴影部分的面积是（）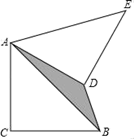

A、2 $\sqrt{3}$ ﹣2 B、2 $\sqrt{3}$ C、 $\sqrt{3}$ ﹣1 D、4 $\sqrt{3}$

查看试题解析
9. 甲、乙两人分别从距目的地6千米和10千米的两地同时出发，甲、乙的速度比是3：4，结果甲比乙提前20分钟到达目的地，求甲、乙的速度．若设甲的速度为3x千米/时，乙的速度为4x千米/时．则所列方程是（）

A、 $\frac{6}{3 x}$ +20= $\frac{10}{4 x}$ B、 $\frac{6}{3 x}$ ＝ $\frac{10}{4 x}$ +20 C、 $\frac{6}{3 x}$ + $\frac{20}{60}$ ＝ $\frac{10}{4 x}$ D、 $\frac{6}{3 x}$ ＝ $\frac{10}{4 x}$ + $\frac{20}{60}$

查看试题解析
10. 某工厂2015年产品的产量为100吨，该产品产量的年平均增长率为x（x＞0），设2017年该产品的产量为y吨，则y关于x的函数关系式为（）

A、y＝100（1﹣x）² B、y＝100（1+x）² C、y＝ $\frac{100}{{(1 + x)}^{2}}$ D、y＝100+100（1+x）+100（1+x）²

查看试题解析

二、填空题

11. 分解因式：x²﹣4x= ．

查看试题解析
12. 已知实数a、b都是比2小的数，其中a是整数，b是无理数，请根据要求，分别写出一个a、b的值：a＝， b＝．

查看试题解析
13. 一个多边形的每个外角都等于72°，则这个多边形的边数为．

查看试题解析
14. 扇形的圆心角为60°，弧长为4πcm ，则此扇形的面积等于cm² ．

查看试题解析
15. 已知一组数据是3，4，7，a ，中位数为4，则a＝．

查看试题解析
16. 已知，Rt△ABC中，∠ACB＝90°，AC＝5，BC＝12，点D在边AB上，以AD为直径的⊙O ，与边BC有公共点E ，则AD的最小值是．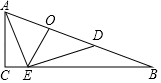

查看试题解析

三、解答题

17. 计算：( $\frac{1}{2}$ )^﹣²﹣ $\sqrt{9}$ +（ $\sqrt{3}$ ﹣4）⁰﹣ $\sqrt{2}$ cos45°．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 2 x + 1 ⩾ - 1 \\ x + 1 > 4 (x - 2) \end{array}$

查看试题解析
19. 如图1，点D、E、F、G分别为线段AB、OB、OC、AC的中点．

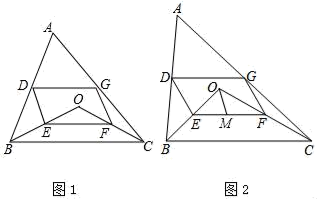(1)、求证：四边形DEFG是平行四边形；

(2)、如图2，若点M为EF的中点，BE：CF：DG＝2：3： $\sqrt{13}$ ，求证：∠MOF＝∠EFO ．

查看试题解析
20. 中华文明，源远流长；中华汉字，寓意深广．为了传承中华民族优秀传统文化，我市某中学举行“汉字听写”比赛，赛后整理参赛学生的成绩，将学生的成绩分为A ， B ， C ， D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整．

请你根据统计图解答下列问题：

(1)、参加比赛的学生共有名；

(2)、在扇形统计图中，m的值为，表示“D等级”的扇形的圆心角为度；

(3)、组委会决定从本次比赛获得A等级的学生中，选出2名去参加全市中学生“汉字听写”大赛．已知A等级学生中男生有1名，请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率．

查看试题解析
21. 已知：∠MAN和线段a ．
求作：菱形ABCD ，使顶点B ， D分别在射线AM ， AN上，且对角线AC＝a ．

查看试题解析
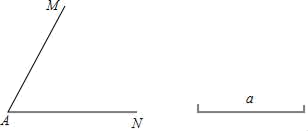22. 在平面直角坐标系xOy中，直线y＝kx+b(k＜0)，经过点(6，0)，且与坐标轴围成的三角形的面积是9，与函数y＝ $\frac{m}{x}$ (x＞0)的图象G交于A ， B两点．

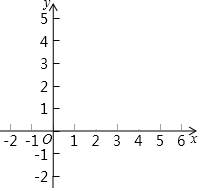(1)、求直线的表达式；

(2)、横、纵坐标都是整数的点叫作整点．记图象G在点A、B之间的部分与线段AB围成的区域(不含边界)为W ．
①当m＝2时，直接写出区域W内的整点的坐标；

②若区域W内恰有3个整数点，结合函数图象，求m的取值范围．

查看试题解析
23. 为了保护环境，某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆，其中A种型号每辆价格为a万元，每年节省油量为2.4万升；B种型号每辆价格为b万元，每年节省油量为2.2万升：经调查，购买一辆A型车比购买一辆B型车多20万元，购买2辆A型车比购买3辆B型车少60万元．

(1)、请求出a和b；

(2)、若购买这批混合动力公交车每年能节省22.4万升汽油，求购买这批混合动力公交车需要多少万元？

查看试题解析

24. 如图，点P是

\overset{⌢}{A B}

所对弦AB上一动点，点Q是

\overset{⌢}{A B}

与弦AB所围成的图形的内部的一定点，作射线PQ交

\overset{⌢}{A B}

于点C ，连接BC ．已知AB＝6cm ，设A ， P两点间的距离为xcm ， P ， C两点间的距离为y₁cm ， B ， C两点间的距离为y₂cm ．（当点P与点A重合时，x的值为0）．

小平根据学习函数的经验，分别对函数y₁ ， y₂随自变量x的变化而变化的规律进行了探究．

下面是小平的探究过程，请补充完整：

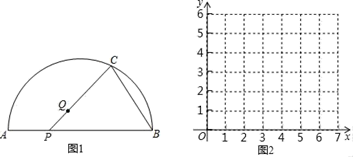(1)、按照下表中自变量x的值进行取点、画图、测量，分别得到了y与x的几组对应值；

x/cm	0	1	2	3	4	5	6
y₁/cm	5.37	4.06	2.83	m	3.86	4.83	5.82
y₂/cm	2.68	3.57	4.90	5.54	5.72	5.79	5.82

经测量m的值是（保留一位小数）．

(2)、在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x ， y₁），（x ， y₂），并画出函数y₁ ， y₂的图象；

(3)、结合函数图象，解决问题：当△BCP为等腰三角形时，AP的长度约为cm ．

查看试题解析

25. 已知二次函数y＝x²﹣（k+1）x+ $\frac{1}{4}$ k²+1与x轴有交点．

(1)、求k的取值范围；

(2)、方程x²﹣（k+1）x+ $\frac{1}{4}$ k²+1＝0有两个实数根，分别为x₁ ， x₂ ，且方程x₁²+x₂²+15＝6x₁x₂ ，求k的值，并写出y＝x²﹣（k+1）x+ $\frac{1}{4}$ k²+1的代数解析式．

查看试题解析