福建省泉州市惠安县2018-2019学年中考数学一模考试试卷
试卷更新日期:2019-07-09 类型:中考模拟
一、单选题
-
1. 下列各数是无理数的是( )A、0 B、 C、1.010010001… D、﹣2. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
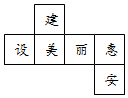 A、美 B、丽 C、惠 D、安3. 下列运算正确的是( )A、3﹣1=﹣3 B、 =±3 C、(ab2)3=a3b6 D、a6÷a2=a34. 不等式2x﹣3>﹣5的解集在数轴上表示正确的是( )A、
A、美 B、丽 C、惠 D、安3. 下列运算正确的是( )A、3﹣1=﹣3 B、 =±3 C、(ab2)3=a3b6 D、a6÷a2=a34. 不等式2x﹣3>﹣5的解集在数轴上表示正确的是( )A、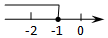 B、
B、 C、
C、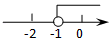 D、
D、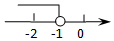 5. 在下列对称图形中,对称轴的条数最少的图形是( )A、圆 B、等边三角形 C、正方形 D、正六边形6. 学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )
5. 在下列对称图形中,对称轴的条数最少的图形是( )A、圆 B、等边三角形 C、正方形 D、正六边形6. 学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )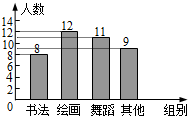 A、0.1 B、0.15 C、0.25 D、0.37. 如图将一把直尺,含有60°的直角三角板和光盘如图摆放,已知点A为60°角与直尺交点,AB=2,则光盘的直径是( )
A、0.1 B、0.15 C、0.25 D、0.37. 如图将一把直尺,含有60°的直角三角板和光盘如图摆放,已知点A为60°角与直尺交点,AB=2,则光盘的直径是( ) A、2 B、2 C、4 D、48. 某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如用9枚图钉将4张作品钉在墙上如图).若有28枚图钉可供选用,则最多可以展示绘画作品( )
A、2 B、2 C、4 D、48. 某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如用9枚图钉将4张作品钉在墙上如图).若有28枚图钉可供选用,则最多可以展示绘画作品( ) A、16张 B、18张 C、20张 D、21张9. 如图,在平面直角坐标系中,过格点A,B,C作一圆弧,将点B与下列格点分别连线,当连线与圆弧相切时,该格点的坐标是( )
A、16张 B、18张 C、20张 D、21张9. 如图,在平面直角坐标系中,过格点A,B,C作一圆弧,将点B与下列格点分别连线,当连线与圆弧相切时,该格点的坐标是( )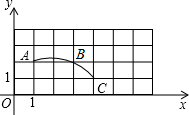 A、(0,3) B、(5,1) C、(2,3) D、(6,1)10. 已知二次函数y=ax2+bx+c,其函数y与自变量x之间的部分对应值如表所示:
A、(0,3) B、(5,1) C、(2,3) D、(6,1)10. 已知二次函数y=ax2+bx+c,其函数y与自变量x之间的部分对应值如表所示:X
…
﹣1
2
3
…
Y
…
0
0
4
…
则可求得 (4a﹣2b+c)的值是( )
A、8 B、﹣8 C、4 D、﹣4二、填空题
-
11. 计算:20190﹣2= .12. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为 .13. 某班八位女同学的身高分别为(单位:厘米)156、158、162、163、165、165、168、169,则这组数据的中位数为 .14. 如图,四边形ACDF是正方形,∠CEA和∠ABF都是直角,且点E、A、B三点共线,若AB=2,则阴影部分的面积是 .
 15. 任何一个无限循环小数都可以写成分数的形式.我们以无限循环小数 为例说明如下:设 =x,由 =0.555…可知,10x=5.555…,所以10x﹣x=5,解方程得x= ,于是, = .请你把 写成分数的形式是 .16. 若直线y=﹣3x+b与双曲线 在1≤x≤4范围内有公共点,则b的取值范围是 .
15. 任何一个无限循环小数都可以写成分数的形式.我们以无限循环小数 为例说明如下:设 =x,由 =0.555…可知,10x=5.555…,所以10x﹣x=5,解方程得x= ,于是, = .请你把 写成分数的形式是 .16. 若直线y=﹣3x+b与双曲线 在1≤x≤4范围内有公共点,则b的取值范围是 .三、解答题
-
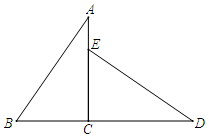
17. 先化简,再求值: ,其中m= .18. 解不等式组,并把它们的解集在数轴上表示出来: .19. 如图,AC⊥BD,DE交AC于E,AB=DE,∠A=∠D.求证:AC=AE+BC.
 20. 我国古代有一道著名的算术题,原文为:吾问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空,问几房几客?意为:一批客人来到李三的旅店住宿,如果每个房间住7人,那么有7位客人没房住;如果每个房间住9人,那么有1间空房,问共有多少位客人?多少间房?请你用初中数学知识方法求出上述问题的解。21. 求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.解答要求如下:
20. 我国古代有一道著名的算术题,原文为:吾问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空,问几房几客?意为:一批客人来到李三的旅店住宿,如果每个房间住7人,那么有7位客人没房住;如果每个房间住9人,那么有1间空房,问共有多少位客人?多少间房?请你用初中数学知识方法求出上述问题的解。21. 求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.解答要求如下: (1)、对于图中△ABC,用尺规作出一条中位线DE;(不必写作法,但应保留作图痕迹)(2)、根据(1)中作出的中位线,写出已知,求证和证明过程.22. 如图,在直角坐标系中,点P的坐标为(2,0),⊙P与x轴相交于原点O和点A,又B、C两点的坐标分别为(0,b),(﹣1,0).
(1)、对于图中△ABC,用尺规作出一条中位线DE;(不必写作法,但应保留作图痕迹)(2)、根据(1)中作出的中位线,写出已知,求证和证明过程.22. 如图,在直角坐标系中,点P的坐标为(2,0),⊙P与x轴相交于原点O和点A,又B、C两点的坐标分别为(0,b),(﹣1,0).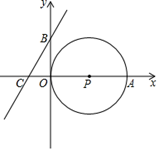 (1)、当b=2时,求经过B、C两点的直线解析式;(2)、当B点在y轴上运动时,直线BC与⊙P位置关系如何?并求出相应位置b的值23. 为弘扬“绿水青山就是金山银山”精神,某地区鼓励农户利用荒坡种植果树,某农户考察三种不同的果树苗A、B、C,经引种试验后发现,引种树苗A的自然成活率为0.8,引种树苗B、C的自然成活率均为0.9.(1)、若引种树苗A、B、C各10棵.
(1)、当b=2时,求经过B、C两点的直线解析式;(2)、当B点在y轴上运动时,直线BC与⊙P位置关系如何?并求出相应位置b的值23. 为弘扬“绿水青山就是金山银山”精神,某地区鼓励农户利用荒坡种植果树,某农户考察三种不同的果树苗A、B、C,经引种试验后发现,引种树苗A的自然成活率为0.8,引种树苗B、C的自然成活率均为0.9.(1)、若引种树苗A、B、C各10棵.①估计自然成活的总棵数;
②利用①的估计结论,从没有自然成活的树苗中随机抽取两棵,求抽到的两棵都是树苗A的概率:
(2)、该农户决定引种B种树苗,引种后没有自然成活的树苗中有75%的树苗可经过人工栽培技术处理,处理后成活的概率为0.8,其余的树苗不能成活.若每棵树苗引种最终成活后可获利300元,不成活的每棵亏损50元,该农户为了获利不低于20万元,问至少引种B种树苗多少棵?24. 如图1,已知⊙O是ΔADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC. (1)、求证:AC=BC;(2)、如图2,在图1的基础上做⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH//BC,求∠ACF的度数;(3)、在(2)的条件下,若ΔABD的面积为 ,ΔABD与ΔABC的面积比为2:9,求CD的长.25. 已知抛物线y=ax2﹣bx.(1)、若此抛物线与直线y=x只有一个公共点,且向右平移1个单位长度后,刚好过点(3,0).
(1)、求证:AC=BC;(2)、如图2,在图1的基础上做⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH//BC,求∠ACF的度数;(3)、在(2)的条件下,若ΔABD的面积为 ,ΔABD与ΔABC的面积比为2:9,求CD的长.25. 已知抛物线y=ax2﹣bx.(1)、若此抛物线与直线y=x只有一个公共点,且向右平移1个单位长度后,刚好过点(3,0).①求此抛物线的解析式;
②以y轴上的点P(0,n)为中心,作该抛物线关于点P对称的抛物线y',若这两条抛物线有公共点,求n的取值范围;
(2)、若a>0,将此抛物线向上平移c个单位(c>0),当x=c时,y=0;当0<x<c时,y>0.试比较ac与1的大小,并说明理由.