山西省阳泉市平定县2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2019-07-09 类型：期末考试

进入出卷网下载

一、单选题

1. 16的平方根是（　　）

A、4 B、±4 C、﹣4 D、±8

查看试题解析
2. 在平面直角坐标系中，点（5，﹣3）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 是二元一次方程3x﹣my＝5的一组解，则m的值为（）

A、﹣2 B、2 C、﹣ $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
4. 某中学开展“阳光体育一小时”活动，根据学校实际情况，决定开设①踢毽子；②篮球；③跳绳；④乒乓球四种运动项目．为了解学生最喜欢哪一种运动项目，随机抽取了一部分学生进行调查，并将调查结果绘制成如下不完整的两个统计图，依据图中信息，得出下列结论中正确的是（）

A、本次共调查300名学生 B、扇形统计图中，喜欢篮球项目的学生部分所对应的扇形圆心角大小为45° C、喜欢跳绳项日的学生人数为60人 D、喜欢篮球项目的学生人数为30人

查看试题解析
5. 点P(m+3，m+1)在直角坐标系的x轴上，则点P的坐标为（）

A、(0，﹣2) B、(2，0) C、(4，0) D、(0，﹣4)

查看试题解析
6.
如图，AB∥CD，∠1=58°，FG平分∠EFD，则∠FGB的度数等于（）

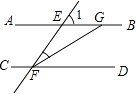A、122° B、151° C、116° D、97°

查看试题解析
7. 不等式组 ${\begin{array}{l} 4 x > 2 \\ - \frac{x}{3} + 1 \geq 0 \end{array}$ 的整数解为（）

A、0，1，2，3 B、1，2，3 C、2，3 D、3

查看试题解析
8. 我国古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米1534石，验得米内夹谷，抽样取米一把，数得254粒内夹谷28粒，则这批米内夹谷约为（）

A、134石 B、169石 C、338石 D、1365石

查看试题解析
9. 如图，小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏，他将纸片沿EF折叠后，D ， C两点分别落在点D′，C′的位置，∠DEF＝∠D′EF ，并利用量角器量得∠EFB＝66°，则∠AED′的度数为（）

A、66° B、132° C、48° D、38°

查看试题解析

10. 某市居民用电的电价实行阶梯收费，收费标准如下表：

一户居民每月用电量x(单位：度)	电费价格(单位：元/度)
0＜x≤200	0.48
200＜x≤400	0.53
x＞400	0.78

七月份是用电高峰期，李叔计划七月份电费支出不超过200元，直接写出李叔家七月份最多可用电的度数是（）

A、100 B、396 C、397 D、400

查看试题解析

二、填空题

11. 如果把方程3x+y＝2写成用含x的代数式表示y的形式，那么y＝．

查看试题解析
12. 已知A（2，﹣3），先将点A向左平移3个单位，再向上平移2个单位得到点B，则点B的坐标是．

查看试题解析
13. 如图，一把长方形直尺沿直线断开并错位，点E ， D ， B ， F在同一条直线上．如果∠ADE＝126°，那么∠DBC＝°．

查看试题解析
14. 关于x的不等式ax＞b的解集是x＜ $\frac{b}{a}$ ，写出一组满足条件的a ， b的值：a＝．

查看试题解析
15. 阅读下面材料：在数学课上，老师提出如下问题：
作图：过直线外一点作已知直线的平行线．

已知：直线l及其外一点A(如图1)．

求作：l的平行线，使它经过点A ．

小凡利用两块形状相同的三角尺进行如下操作：

如图2所示：

⑴用第一块三角尺的一条边贴住直线l ，第二块三角尺的一条边紧靠第一块三角尺；

⑵将第二块三角尺沿第一块三角尺移动，使其另一边经过点A ，沿这边作出直线AB ，所以，直线AB即为所求．

老师说：“小凡的作法正确”

请回答：小凡的作图依据是．

查看试题解析

三、解答题

16.

(1)、计算： $\sqrt{{(- 1)}^{2}}$ + $\sqrt{\frac{1}{4}}$ ×(﹣2)²﹣ $\sqrt[3]{- 27}$ ．

(2)、解不等式组 ${\begin{array}{l} 3 x < x + 8 \\ 4 (x + 1) \leq 7 x + 10 \end{array}$ ，并把不等式组的解集在数轴上表示出来．

查看试题解析
17. 已知 ${\begin{array}{l} x = - 2 \\ y = - 8 \end{array}$ 和 ${\begin{array}{l} x = 3 \\ y = 7 \end{array}$ 是关于x ， y的二元一次方程y＝kx+b的解，求k ， b的值．

查看试题解析
18. 如图，平面直角坐标系中，已知点A（﹣3，3），B（﹣5，1），C（﹣2，0），P（a，b）是△ABC的边AC上任意一点，△ABC经过平移后得到△A₁B₁C₁ ，点P的对应点为P₁（a+6，b﹣2 ）．

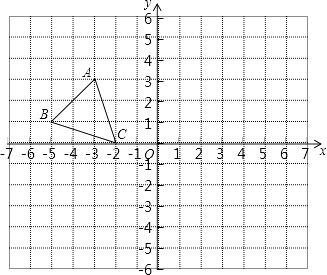(1)、直接写出点A₁ ， B₁ ， C₁的坐标．

(2)、在图中画出△A₁B₁C₁ ．

(3)、连接A A₁ ，求△AOA₁的面积．

查看试题解析
19. 学完二元一次方程组的应用之后，老师写出了一个方程组如下： ${\begin{array}{l} 2 x - y = 5 \\ 4 x + 3 y = 40 \end{array}$ ，要求把这个方程组赋予实际情境．
小军说出了一个情境：学校有两个课外小组，书法组和美术组，其中书法组的人数的二倍比美术组多5人，书法组平均每人完成了4幅书法作品，美术组平均每人完成了3幅美术作品，两个小组共完成了40幅作品，问书法组和美术组各有多少人？

小明通过验证后发现小军赋予的情境有问题，请找出问题在哪？

查看试题解析

20. 诗词是我国古代文化中的瑰宝，某市教育主管部门为了解本市初中生对诗词的学习情况，举办了一次“中华诗词”背诵大赛，随机抽取了部分同学的成绩(x为整数，总分100分)，绘制了如下尚不完整的统计图表．

组别	成绩分组(单位：分)	频数
A	50≤x＜60	40
B	60≤x＜70	a
C	70≤x＜80	90
D	80≤x＜90	b
E	90≤x＜100	100
合计		c

根据以上信息解答下列问题：

(1)、统计表中a＝， b＝， c＝；

(2)、扇形统计图中，m的值为， “E”所对应的圆心角的度数是(度)；

(3)、若参加本次大赛的同学共有4000人，请你估计成绩在80分及以上的学生大约有多少人？

查看试题解析

21. 已知：如图，点C在∠AOB的一边OA上，过点C的直线DE∥OB ， CF平分∠ACD ， CG⊥CF于点C ．

(1)、若∠O＝40°，求∠ECF的度数；

(2)、求证：CG平分∠OCD ．

查看试题解析
22. 为了更好改善河流的水质，治污公司决定购买10台污水处理设备.现有A，B两种型号的设备，其中每台的价格，月处理污水量如下表：经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元.

A型

B型

价格(万元/台)

a

b

处理污水量(吨/月)

240

200

(1)、求a，b的值；

(2)、治污公司经预算购买污水处理设备的资金不超过105万元，你认为该公司有哪几种购买方案；

(3)、在(2)的条件下，若每月要求处理污水量不低于2040吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案.

查看试题解析
23. 问题情境：如图1，AB∥CD ， ∠PAB＝130°，∠PCD＝120°，求∠APC的度数．小明的思路是：过点P作PE∥AB ，通过平行线性质来求∠APC ．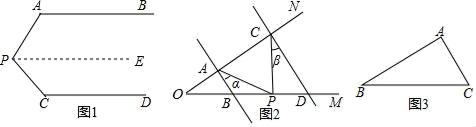

(1)、按小明的思路，请你求出∠APC的度数；

(2)、问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB＝α，∠PCD＝β，当点P在B，D两点之间运动时，问∠APC与α，β之间有何数量关系？请说明理由；

(3)、联想拓展：在(2)的条件下，如果点P在B ， D两点外侧运动时(点P与点O ， B ， D三点不重合)，请直接写出∠APC与α，β之间的数量关系；

(4)、解决问题：我们发现借助构造平行线的方法可以帮我们解决许多问题，随着以后的学习你还会发现平行线的许多用途．试构造平行线解决以下问题．
已知：如图3，三角形ABC ，求证：∠A+∠B+∠C＝180°

查看试题解析

	A型	B型
价格(万元/台)	a	b
处理污水量(吨/月)	240	200