福建省龙岩市五县、区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-09 类型:期末考试
一、单选题
-
1. -8的立方根是( )A、-2 B、2 C、±2 D、4
-
2. 下列各数中,界于6和7之间的数是( )A、 B、 C、 D、
-
3. 若y轴上的点A到x轴的距离为3,则点A的坐标为( )A、(3,0) B、(3,0)或(-3,0) C、(0,3) D、(0,3)或(0,-3)
-
4. 不等式组 的解集是( )A、-5≤x<3 B、-5<x≤3 C、x≥-5 D、x<3
-
5. 下列问题中,应采用抽样调查的是( )A、企业招聘,对应聘人员进行面试 B、了解某班学生的身高情况 C、调查春节联欢晚会的收视率 D、了解某校七年级第二学期期末考试各班的数学科平均成绩
-
6. 已知a∥b , 将等腰直角三角形ABC按如图所示的方式放置,其中锐角顶点B , 直角顶点C分别落在直线a , b上,若∠1 15°,则∠2的度数是( )
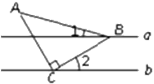 A、15° B、22.5° C、30° D、45°
A、15° B、22.5° C、30° D、45° -
7. 如下图所示,下列各组图形中,一个图形经过平移能得到另一个图形的是( )A、
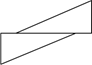 B、
B、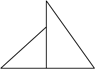 C、
C、 D、
D、
-
8. 如图,已知AD∥BC,∠C=30°,∠ADB:∠BDC=1:2,那么∠ADB等于( )
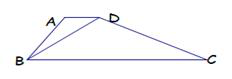 A、45° B、30° C、50° D、36°
A、45° B、30° C、50° D、36° -
9. 对于实数 ,我们规定 表示不大于 的最大整数,例如 , , ,若 ,则 的取值可以是( )A、40 B、45 C、56 D、51
-
10. 关于x、y的方程组 的解为整数,则满足这个条件的整数m的个数有( )A、4个 B、3个 C、2个 D、无数个
二、填空题
-
11. 计算: .
-
12. 请写出一个比2大且比4小的无理数:.
-
13. 已知 (y-3)2=0,则:x+y的值为
-
14. 如图,把长方形ABCD沿EF对折,若∠1=500 , 则∠AEF的度数等于.
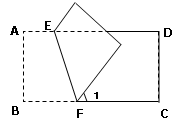
-
15. 如图,在平面直角坐标系中,若▱ABCD的顶点A,B,C的坐标分别是(2,3),(1,-1),(7,-1),则点D的坐标是 .

-
16. 古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,则第1007个三角数与第1009个三角数的差为.
三、解答题
-
17. 计算:
-
18. 解不等式,并把它的解集在数轴上表示出来.
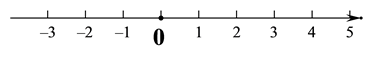
-
19. 解方程组:
-
20. 如图:O为直线AB上一点, ,OC是 的平分线.求: 的度数
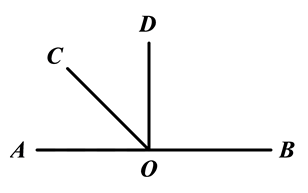
-
21. 某企业工会开展“一周工作量完成情况”调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图1和图2所示的不完整统计图.
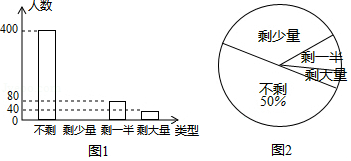 (1)、被调查员工的人数为人:(2)、把条形统计图补充完整;(3)、若该企业有员工10000人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
(1)、被调查员工的人数为人:(2)、把条形统计图补充完整;(3)、若该企业有员工10000人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人? -
22. 在图中描出A(-4,4),B(0,4),C(2,1),D(-2,1)四个点,线段AB、CD有什么位置关系?顺次连接A,B,C,D四点,求四边形ABCD的面积.

-
23. 我国古代数学著作《九章算术》中有这样一题,原文是:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何.”意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,是古代的一种容量单位),1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛?请解答.
-
24. 某公园的门票每张20元,一次性使用.考虑到人们的不同需求,也为了吸引更多的游客,该公园除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法.年票分A,B,C三类,A类年票每张240元,持票进入该园区时,无需再购买门票;B类年票每张120元,持票者进入该园区时,需再购买门票,每次4元;C类年票每张80元,持票者进入该园区时,需再购买门票,每次6元.(1)、如果只能选择一种购买年票的方式,并且计划在一年中花费160元在该公园的门票上,通过计算,找出可进入该园区次数最多的方式.(2)、一年中进入该公园超过多少次时,A类年票比较合算?
-
25. 如图,在平面直角坐标系xOy中,点A(a , 0),B(c , c),C(0,c),且满足 ,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.

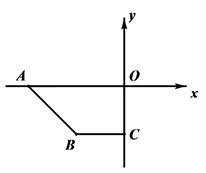 (1)、直接写出点B的坐标,AO和BC位置关系是;(2)、当P、Q分别是线段AO , OC上时,连接PB , QB , 使 ,求出点P的坐标;(3)、在P、Q的运动过程中,当∠CBQ=30°时,请探究∠OPQ和∠PQB的数量关系,并说明理由.
(1)、直接写出点B的坐标,AO和BC位置关系是;(2)、当P、Q分别是线段AO , OC上时,连接PB , QB , 使 ,求出点P的坐标;(3)、在P、Q的运动过程中,当∠CBQ=30°时,请探究∠OPQ和∠PQB的数量关系,并说明理由.
