福建省龙岩市上杭县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2019-07-09 类型:期末考试
一、单选题
-
1. 下列工具中,有对顶角的是( )A、
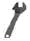 B、
B、 C、
C、 D、
D、 2. 点P(5,-3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列调查中,适合的是( )A、《新闻联播》电视栏目的收视率,采用全面调查方式 B、为了精确调查你所在班级的同学的身高,采用抽样调查方式 C、习主席视察长江水域建设情况,环保部门为调查长江某段水域的水质情况,采用抽样调查方式 D、调查一个乡镇学生家庭的收入情况,采用全面调查方式4. 下列各式正确的是( )A、 B、 C、 D、5. 如图,不等式组 的解集在数轴上表示正确的是( )A、
2. 点P(5,-3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列调查中,适合的是( )A、《新闻联播》电视栏目的收视率,采用全面调查方式 B、为了精确调查你所在班级的同学的身高,采用抽样调查方式 C、习主席视察长江水域建设情况,环保部门为调查长江某段水域的水质情况,采用抽样调查方式 D、调查一个乡镇学生家庭的收入情况,采用全面调查方式4. 下列各式正确的是( )A、 B、 C、 D、5. 如图,不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、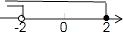 D、
D、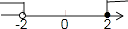 6. 已知a>b , 下列不等式变形错误的是( )A、a+2>b+2 B、a﹣2>b﹣2 C、2a>2b D、2﹣a>2﹣b7. 如图,已知AB∥CD , BC平分∠ABE , ∠C=33°,则∠CEF的度数是( )
6. 已知a>b , 下列不等式变形错误的是( )A、a+2>b+2 B、a﹣2>b﹣2 C、2a>2b D、2﹣a>2﹣b7. 如图,已知AB∥CD , BC平分∠ABE , ∠C=33°,则∠CEF的度数是( )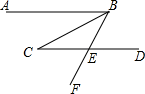 A、66° B、49° C、33° D、16°8. 某种商品的进价为80元,出售时标价为120元,后来由于该商品积压,商店准备打折出售,但要保证利润率不低于5%,则至多可打( )A、六折 B、七折 C、八折 D、九折9. 已知a , b都是正整数,且a> ,b< ,则a-b的最小值是( )A、1 B、2 C、3 D、410. 已知 和 是关于x , y的方程kx+2y=5的两组解,且0<k<4则n的值可以是( )A、3 B、4 C、5 D、6
A、66° B、49° C、33° D、16°8. 某种商品的进价为80元,出售时标价为120元,后来由于该商品积压,商店准备打折出售,但要保证利润率不低于5%,则至多可打( )A、六折 B、七折 C、八折 D、九折9. 已知a , b都是正整数,且a> ,b< ,则a-b的最小值是( )A、1 B、2 C、3 D、410. 已知 和 是关于x , y的方程kx+2y=5的两组解,且0<k<4则n的值可以是( )A、3 B、4 C、5 D、6二、填空题
-
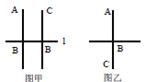
11. 把二元一次方程3x-y=2改写成含x的式子表示y的形式: .12. 某校七年级(1)班60名学生在一次单元测试中,优秀人数是20人,在扇形统计图中,表示这部分同学的扇形圆心角是度.13. 若x的一半与1的和为非负数,且x<0,则x可取的所有整数解的和是 .14. 在- , , , , 这5个数中,最小的有理数是 .15. 已知直线AB , CB , l在同一平面内,若AB⊥l , 垂足为B , CB⊥l , 垂足也为B , 则正确的图形可以是如图中的图(填甲或乙),你选择的依据是(写出你学过的一条公理).
 16. 小明有一根3米长的绳子,第一次截去 米,第二次又截去 米,这根绳子还剩米
16. 小明有一根3米长的绳子,第一次截去 米,第二次又截去 米,这根绳子还剩米三、解答题
-
17.(1)、计算: ﹣ -2( -1)- .(2)、解方程组:18. 解不等式 ,并把它的解集在数轴上表示出来.19. 《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
20. 如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.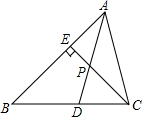 21. 先化简,再求值: ,其中m、n满足:2n+1和5+n是正数m的两个平方根.22. 某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.
21. 先化简,再求值: ,其中m、n满足:2n+1和5+n是正数m的两个平方根.22. 某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.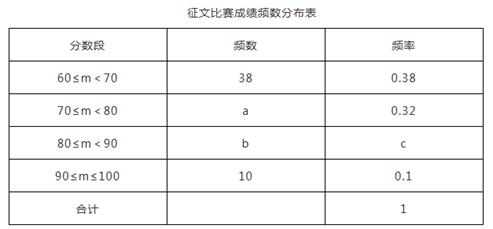
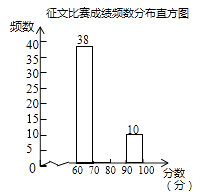
请根据以上信息,解决下列问题:
(1)、征文比赛成绩频数分布表中c的值是;(2)、补全征文比赛成绩频数分布直方图;(3)、若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.23.(1)、我们知道“三角形三个内角的和为180°”.现在我们用平行线的性质来证明这个结论是正确的.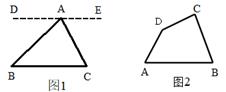
已知:∠BAC、∠B、∠C是△ABC的三个内角,如图1.
求证:∠BAC+∠B+∠C=180°证明:过点A作直线DE∥BC(请你把证明过程补充完整)
(2)、请你用(1)中的结论解答下面问题:如图2,已知四边形ABCD , 求∠A+∠B+∠C+∠D的度数.
24. 某县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)、求A、B两种型号的电风扇的销售单价;(2)、若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?(3)、在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.25. 在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.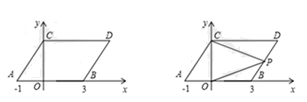 (1)、求点C,D的坐标及四边形ABDC的面积S四边形ABDC;(2)、在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由;(3)、点P是直线BD上一个动点,连接PC、PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD、∠POB的数量关系
(1)、求点C,D的坐标及四边形ABDC的面积S四边形ABDC;(2)、在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由;(3)、点P是直线BD上一个动点,连接PC、PO,当点P在直线BD上运动时,请直接写出∠OPC与∠PCD、∠POB的数量关系