山西省孝义市2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2019-07-09 类型：期中考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、2 B、﹣2 C、±2 D、 $\sqrt{2}$

查看试题解析
2. 如图，直线 $a / / b$ ，直线 $∠ 1 = 115 °$ ，则 $∠ 2$ 的度数为（）

A、 $115 °$ B、 $75 °$ C、 $65 °$ D、 $55 °$

查看试题解析
3. 根据下列表述，能确定位置的是（）

A、孝义市府前街 B、南偏东 $45 °$ C、美莱登国际影城3排 D、东经 $116.4 °$ ，北纬 $39.9 °$

查看试题解析
4. 下列说法正确的有（）
①对顶角相等；②同位角相等；③若两个角不相等，则这两个角一定不是对顶角；④若两个角不相等，则这两个角一定不是同位角.

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，现要从村庄 $P$ 修建一条连接公路 $A B$ 的最短小路，过点 $P$ 作 $P C ⊥ A B$ 于点 $C$ ，沿 $P C$ 修建公路就能满足小路最短，这样做的依据是（）

A、两点确定一条直线 B、两点之间，线段最短 C、垂线段最短 D、平面内，过一点有且只有一条直线与已知直线垂直

查看试题解析
6. 下列结论正确的是（）

A、 $- \sqrt{{(- 6)}^{2}} = - 6$ B、 ${(- \sqrt{3})}^{2} = 9$ C、 $\sqrt{{(- 16)}^{2}} = \pm 6$ D、 $- {(- \sqrt{2})}^{2} = \sqrt{2}$

查看试题解析
7. 在平面直角坐标系内，点 $P (x, x + 5)$ 的位置一定不在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 如图，下列能判定 $A B / / C D$ 的条件的个数是（）

① $∠ B + ∠ B C D = 180 °$ ② $∠ 2 = ∠ 3$ ③ $∠ 1 = ∠ 4$ ④ $∠ B = ∠ 5$

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 公元前5世纪，毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 $\sqrt{2}$ ，导致了第一次数学危机. $\sqrt{2}$ 是无理数的证明如下：
假设 $\sqrt{2}$ 是有理数，那么它可以表示成 $\frac{q}{p}$ （ $p$ 与 $q$ 是互质的两个正整数）.于是 ${(\frac{q}{p})}^{2} = {(\sqrt{2})}^{2} = 2$ ，所以， $q^{2} = 2 p^{2}$ .于是 $q^{2}$ 是偶数，进而 $q$ 是偶数.从而可设 $q = 2 m$ ，所以 ${(2 m)}^{2} = 2 p^{2}$ ， $p^{2} = 2 m^{2}$ ，于是可得 $p$ 也是偶数.这与“ $p$ 与 $q$ 是互质的两个正整数”矛盾，从而可知“ $\sqrt{2}$ 是有理数”的假设不成立，所以， $\sqrt{2}$ 是无理数.这种证明“ $\sqrt{2}$ 是无理数”的方法是（）

A、综合法 B、反证法 C、举反例法 D、数学归纳法

查看试题解析
10. 规定以下两种变换：① $f (a, b) = (- a, b)$ ，如 $f (1, 2) = (- 1, 2)$ ；② $g (a, b) = (- a, - b)$ ，如 $g (1, 2) = (- 1, - 2)$ ，.按照以上变换有 $f [g (2, 3)] = f (- 2, - 3) = (2, - 3)$ .则 $g [f (3, 4)]$ =（）

A、 $(3, 4)$ B、 $(3, - 4)$ C、 $(- 3, 4)$ D、 $(- 3, - 4)$

查看试题解析

二、填空题

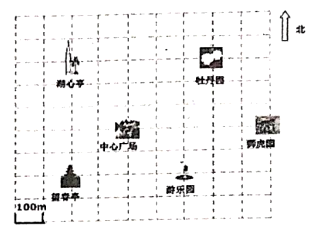
11. 比较大小： $- \sqrt[3]{50}$ $- 4$ （填“ $<$ ”或“ $=$ ”或“ $>$ ”）.

查看试题解析
12. 将命题“内错角相等”，写成“如果……，那么……”的形式：.

查看试题解析
13. 平面直角坐标系的应用十分广泛，用坐标表示地理位置体现了坐标系在实际生活中的应用.不管是出差办事，还是出去旅游，人民都愿意带上一副地图，它给人们出行带来了很大方便.如图是某市地图的一部分.在图中，分别以正东、正北方向为 $x$ 轴， $y$ 轴的正方向建立平面直角坐标系，若表示牡丹园的点的坐标为 $(4 ， 1)$ ，则表示狮虎园的点的坐标为.

查看试题解析
14. 如果a，b是2019的两个平方根，则 $a + b - 2 a b =$ .

查看试题解析
15. 如图，半径为1个单位长度的圆从原点沿数轴向左滚动一周，圆上的一点由原点达到 $O^{'}$ ，点 $O^{'}$ 表示的数是.

查看试题解析
16. 如图，已知 $A B / / D E$ ， $∠ A B C = 135 °$ ， $∠ C D E = 70 °$ ，则 $∠ B C D =$ .

查看试题解析

三、解答题

17.

(1)、计算： $\sqrt{2} (\sqrt{2} - 2) + \sqrt{8}$

(2)、计算： $\sqrt{{(- 5)}^{2}} - \sqrt[3]{- 27} + {(- 2)}^{2} + 4 \div (- \frac{2}{3})$

(3)、已知 ${(x + 1)}^{2} = 16$ ，求 $x$ 的值.

查看试题解析
18. 如图，四边形 $A B C D$ ，点 $E$ 是边 $A B$ 延长线上一点，点 $F$ 是边 $C D$ 延长线上一点，连接 $E F$ ，分别交 $B C$ 和 $A D$ 于点 $G$ 和点 $H$ .已知 $A D / / B C$ ， $∠ A = ∠ C$ .求证： $∠ E = ∠ F$ ，并写出每一步的根据.

查看试题解析
19. 小丽想用一块面积为 $400 c m^{2}$ 的正方形纸片，沿着边的方向裁出一块面积为 $360 c m^{2}$ 的长方形纸片，使它的长宽之比为4:3，他不知道能否裁的出来，正在发愁，请你用所学知识帮小丽分析，能否裁出符合要求的纸片.

查看试题解析
20. 如图，在平面直角坐标系中，已知点 $A (- 2 ， 5)$ ， $B (- 3 ， 3)$ ， $C (1 ， 2)$ ，点 $P (m ， n)$ 是三角形 $A B C$ 边 $B C$ 上任意一点，三角形经过平移后得到三角形 $A_{1} B_{1} C_{1}$ ，点 $P$ 的对应点为 $P_{1} (m + 6 ， n - 2)$ .

(1)、直接写出点 $B_{1}$ 的坐标.

(2)、画出三角形 $A B C$ 平移后的三角形 $A_{1} B_{1} C_{1}$ .

(3)、在 $y$ 轴上是否存在一点 $P$ ，使三角形 $A O P$ 的面积等于三角形 $A B C$ 面积的 $\frac{2}{3}$ ，若存在，请求出点 $P$ 的坐标；若不存在，请说明理由.

查看试题解析

21. 阅读与探究:

在第六章《实数》中，我们学习了平方根和立方根.下表是平方根和立方根的部分内容.

	平方根	立方根
定义	一般地，如果一个数的平方等于 $a$ ，那么这个数叫做 $a$ 的平方根或二次方根.这就是说，如果 $x^{2} = a$ ，那么 $x$ 叫做 $a$ 的平方根.	一般地，如果一个数的立方等于 $a$ ，那么这个数叫做 $a$ 的立方根或三次方根.这就是说，如果 $x^{3} = a$ ，那么 $x$ 叫做 $a$ 的立方根.
运算	求一个数 $a$ 的平方根的运算，叫做开平方.开平方与平方互为逆运算.	求一个数 $a$ 的平立方根的运算，叫做开立方.开立方与立方互为逆运算.
特征	正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根.	正数的立方根是正数；0的立方根是0；负数的立方根是负数.
表示与读法	正数 $a$ 的平方根可以用“ $\pm \sqrt{a}$ ”表示，读作“正负根号 $a$ ”.	一个数 $a$ 的立方根可以用“ $\sqrt[3]{a}$ ”表示，读作“三次根号 $a$ ”.

今天我们类比平方根和立方根的学习方法学习四次方根.

(1)、①填表

$x^{4}$	1	16
$x$	$\pm 1$

②结合上述①中表格情况，类比平方根和立方根的定义，给四次方根下定义：

(2)、思考与归纳

求一个数 $a$ 的四次方根的运算叫做开四次方.开四次方和四次方运算互为逆运算.

①探究：

81的四次方根是； $\frac{16}{81}$ 的四次方根是；

0的四次方根是； $- 4$ （填“有”或“没有”）四次方根.

②归纳：

根据上述①中情况，类比平方根和立方根的特征，归纳四次方根的特征：

③总结：

我们归纳四次方根的特征时，分了正数、0、负数三类进行研究，这种思想叫；（填正确选项的代码）

四次方根的特征是由81， $\frac{16}{81}$ ，0等这几个特殊数的四次方根的特征归纳出来的，这种思想叫.（填正确选项的代码）

A.类比思想

B.分类讨论思想

C.由一般到特殊的思想

D.由特殊到一般的思想

(3)、巩固与应用

类似于平方根和立方根，一个数 $a$ 的四次方根，用符号“ $\pm \sqrt[4]{a}$ ”表示，读作“正、负四次根号 $a$ ”，其中 $a$ 是被开方数，4是根指数.例如 $\pm \sqrt[4]{16}$ 表示16的四次方根， $\pm \sqrt[4]{16} = \pm 2$ .

① $\pm \sqrt[4]{256} =$ （将结果直接填到横线上）.

②比较大小： $\sqrt{3}$ $\sqrt[4]{4}$ （填“”或“”或“”）.

查看试题解析

22. 综合与实践：折纸中的数学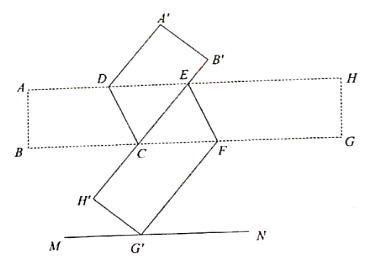
知识背景
我们在七年级上册第四章《几何图形初步》中探究了简单图形折叠问题，并进行了简单的计算与推理.七年级下册第五章我们学习了平行线的性质与判定，今天我们继续探究：折纸中的数学——长方形纸条的折叠与平行线.

(1)、
知识初探
如图1，长方形纸条 $A B G H$ 中， $A B / / G H$ ， $A H / / B G$ ， $∠ A = ∠ B = ∠ G = ∠ H = 90 °$ .将长方形纸条沿直线 $C D$ 折叠，点 $A$ 落在 $A^{'}$ 处，点 $B$ 落在 $B^{'}$ 处， $B^{'} C$ 交 $A H$ 于点 $E$ .若 $∠ E C G = 50 °$ ，求 $∠ C D E$ 的度数.

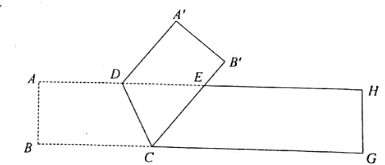(2)、
类比再探
如图2，在图1的基础上将 $∠ H E C$ 对折，点 $H$ 落在直线 $E C$ 上的 $H^{'}$ 处.点 $G$ 落在 $G^{'}$ 处，得到折痕 $E F$ ，则折痕 $E F$ 与 $C D$ 有怎样的位置关系？说明理由.

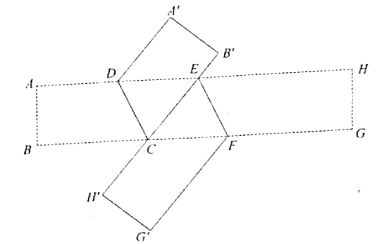(3)、
拓展延伸
如图3，在图2的基础上，过点 $G^{'}$ 作 $B G$ 的平行线 $M N$ ，请你猜想 $∠ E C F$ 和 $∠ H^{'} G^{'} M$ 的数量关系，并说明理由.

查看试题解析