福建省闽侯县2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2019-07-09 类型:期中考试
一、单选题
-
1. 下列各组数中不能作为直角三角形的三边长的是( )A、 , , B、6,8,10 C、7,24,25 D、 ,3,52. 下列各曲线中不能表示y是x函数的是( )A、
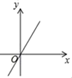 B、
B、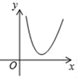 C、
C、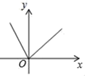 D、
D、 3. 如图,在Rt△ABC中,∠ACB=90°,AB=16,则正方形ADEC和正方形BCFG的面积和为( )
3. 如图,在Rt△ABC中,∠ACB=90°,AB=16,则正方形ADEC和正方形BCFG的面积和为( )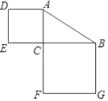 A、16 B、32 C、160 D、2564. 下列条件中,能判断四边形是菱形的是( )A、对角线相等的平行四边形 B、对角线互相垂直且相等的四边形 C、对角线互相平分且垂直的四边形 D、对角线互相垂直的四边形5. 一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,AD=3,CE=5,则CD等于( )
A、16 B、32 C、160 D、2564. 下列条件中,能判断四边形是菱形的是( )A、对角线相等的平行四边形 B、对角线互相垂直且相等的四边形 C、对角线互相平分且垂直的四边形 D、对角线互相垂直的四边形5. 一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,AD=3,CE=5,则CD等于( ) A、3 B、4 C、 D、7. 如图,矩形纸片ABCD中,AD=4,AB=8,把纸片沿直线AC折叠,点B落在E处,AE交DC于点F , 若DF=3,则EF的长为( )
A、3 B、4 C、 D、7. 如图,矩形纸片ABCD中,AD=4,AB=8,把纸片沿直线AC折叠,点B落在E处,AE交DC于点F , 若DF=3,则EF的长为( )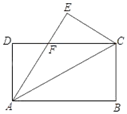 A、3 B、2 C、4 D、58. 如图,在平行四边形ABCD中,∠BAD的平分线交CD于点G , AD=AE . 若AD=5,DE=6,则AG的长是( )
A、3 B、2 C、4 D、58. 如图,在平行四边形ABCD中,∠BAD的平分线交CD于点G , AD=AE . 若AD=5,DE=6,则AG的长是( )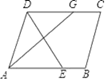 A、6 B、8 C、10 D、129. 已知菱形ABCD , 对角线交点为O , 延长CD至E且CD=DE . 下列判断正确个数是( )
A、6 B、8 C、10 D、129. 已知菱形ABCD , 对角线交点为O , 延长CD至E且CD=DE . 下列判断正确个数是( )⑴∠AOB=90°;(2)AE=2OD;(3)∠OAE=90°;(4)∠AEO=∠CEO .
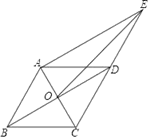 A、1个 B、2个 C、3个 D、4个10. 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.下列结论正确的个数是( )
A、1个 B、2个 C、3个 D、4个10. 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.下列结论正确的个数是( )
(1)t=5时,s=150;(2)t=35时,s=450;(3)甲的速度是30米/分;(4)t=12.5时,s=0.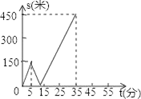
A、1个 B、2个 C、3个 D、4个二、填空题
-
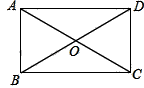
11. 已知点P(a,3)在一次函数y=x+1的图像上,则a= .12. 命题“矩形的对角线相等”的逆命题是 .13. 在矩形ABCD中,两条对角线AC、BD相交于点O , ∠AOB=60°,若AB=4,则AC= .
 14. 勾股定理a2+b2=c2本身就是一个关于a , b , c的方程,显然这个方程有无数解,满足该方程的正整数(a , b , c)通常叫做勾股数.如果三角形最长边c=2n2+2n+1,其中一短边a=2n+1,另一短边为b , 如果a , b , c是勾股数,则b=(用含n的代数式表示,其中n为正整数).15. 若直线y=kx+k+1经过点(m , n+2)和(m+1,2n﹣1),且0<k<2,n是整数,则n= .16. 如图,O为矩形ABCD对角线AC , BD的交点,AB=9,AD=18,M , N是直线BC上的动点,且MN=3,则OM+ON最小值= .
14. 勾股定理a2+b2=c2本身就是一个关于a , b , c的方程,显然这个方程有无数解,满足该方程的正整数(a , b , c)通常叫做勾股数.如果三角形最长边c=2n2+2n+1,其中一短边a=2n+1,另一短边为b , 如果a , b , c是勾股数,则b=(用含n的代数式表示,其中n为正整数).15. 若直线y=kx+k+1经过点(m , n+2)和(m+1,2n﹣1),且0<k<2,n是整数,则n= .16. 如图,O为矩形ABCD对角线AC , BD的交点,AB=9,AD=18,M , N是直线BC上的动点,且MN=3,则OM+ON最小值= .
三、解答题
-
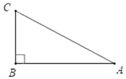
17. 已知Rt△ABC , ∠B=90°,∠A=30°,BC=3,求AC , AB的长.
 18. 如图,在数轴上画出表示 的点(不写作法,但要保留画图痕迹).
18. 如图,在数轴上画出表示 的点(不写作法,但要保留画图痕迹). 19. 如图,在平行四边形ABCD中,点E , F分别为边BC , AD的中点.求证:四边形AECF是平行四边形.
19. 如图,在平行四边形ABCD中,点E , F分别为边BC , AD的中点.求证:四边形AECF是平行四边形.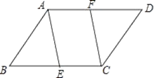 20. 证明:斜边和一条直角边对应相等的两个直角三角形全等.21. 如图,已知菱形ABCD , 四个顶点坐标分别为A(m , n),B(1,2),C(m+ ﹣1,2),D(m+ ,n).求m , n的值.
20. 证明:斜边和一条直角边对应相等的两个直角三角形全等.21. 如图,已知菱形ABCD , 四个顶点坐标分别为A(m , n),B(1,2),C(m+ ﹣1,2),D(m+ ,n).求m , n的值. 22. 如图,矩形纸片ABCD , AB=8,AE=EG=GD=4,AB∥EF∥GH . 将矩形纸片沿BE折叠,得到△BA′E(点A折叠到A′处),展开纸片;再沿BA′折叠,折痕与GH , AD分别交于点M , N , 然后将纸片展开.
22. 如图,矩形纸片ABCD , AB=8,AE=EG=GD=4,AB∥EF∥GH . 将矩形纸片沿BE折叠,得到△BA′E(点A折叠到A′处),展开纸片;再沿BA′折叠,折痕与GH , AD分别交于点M , N , 然后将纸片展开.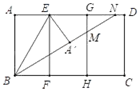 (1)、连接EM , 证明A′M=MG;(2)、设A′M=MG=x , 求x值.23. 旺财水果店每天都会进一些草莓销售,在一周销售过程中他发现每天的销售量y(单位:千克)会随售价x(单位:元/千克)而变化,部分数据记录如表
(1)、连接EM , 证明A′M=MG;(2)、设A′M=MG=x , 求x值.23. 旺财水果店每天都会进一些草莓销售,在一周销售过程中他发现每天的销售量y(单位:千克)会随售价x(单位:元/千克)而变化,部分数据记录如表售价x(单位:元/千克)
30
25
20
每天销售量y(单位:千克)
5
55
105
如果已知草莓每天销量y与售价x(30.5>x>14)满足一次函数关系.
(1)、请根据表格中数据求出这个一次函数关系式;(2)、如果进价为14元/千克,请判断售价分别定为20元/千克和25元/千克,哪天的销售利润更高?24. 如图,已知点A(﹣3,0),点B(0,m),直线l:x=1.直线AB与直线l交于点C , 连结OC . (1)、△OBC的面积与△OAC的面积比是否是定值?如果是,请求出面积比;如果不是,请说明理由.(2)、若m=2,点T在直线l上且TA=TB , 求点T的坐标.25. 如图
(1)、△OBC的面积与△OAC的面积比是否是定值?如果是,请求出面积比;如果不是,请说明理由.(2)、若m=2,点T在直线l上且TA=TB , 求点T的坐标.25. 如图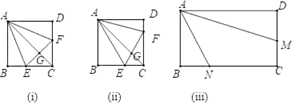 (1)、正方形ABCD , E、F分别在边BC、CD上(不与端点重合),∠EAF=45°,EF与AC交于点G
(1)、正方形ABCD , E、F分别在边BC、CD上(不与端点重合),∠EAF=45°,EF与AC交于点G①如图(i),若AC平分∠EAF , 直接写出线段EF , BE , DF之间等量关系;
②如图(ⅱ),若AC不平分∠EAF , ①中线段EF , BE , DF之间等量关系还成立吗?若成立请证明;若不成立请说明理由
(2)、如图(ⅲ),矩形ABCD , AB=4,AD=8.点M、N分别在边CD、BC上,AN=2 ,∠MAN=45°,求AM的长度.