四川省遂宁市2019年中考数学试卷
试卷更新日期:2019-07-09 类型:中考真卷
一、单选题
-
1. 的值为( )A、 B、 C、 D、22. 下列等式成立的是( )A、 B、 C、 D、3. 如图为正方体的一种平面展开图,各面都标有数字,则数字为 的面与其对面上的数字之积是( )
 A、 B、0 C、 D、4. 某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本是( )A、100 B、被抽取的100名学生家长 C、被抽取的100名学生家长的意见 D、全校学生家长的意见5. 已知关于x的一元二次方程 有一个根为 ,则a的值为( )A、0 B、 C、1 D、6. 如图, 内接于 ,若 , 的半径 ,则阴影部分的面积为( )
A、 B、0 C、 D、4. 某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见,随机对全校100名学生家长进行调查,这一问题中样本是( )A、100 B、被抽取的100名学生家长 C、被抽取的100名学生家长的意见 D、全校学生家长的意见5. 已知关于x的一元二次方程 有一个根为 ,则a的值为( )A、0 B、 C、1 D、6. 如图, 内接于 ,若 , 的半径 ,则阴影部分的面积为( )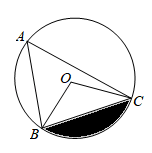 A、 B、 C、 D、7. 如图, 中,对角线 、 相交于点O , 交 于点E , 连接 ,若 的周长为28,则 的周长为( )
A、 B、 C、 D、7. 如图, 中,对角线 、 相交于点O , 交 于点E , 连接 ,若 的周长为28,则 的周长为( )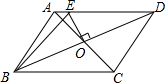 A、28 B、24 C、21 D、148. 关于x的方程 的解为正数,则k的取值范围是( )A、 B、 C、 且 D、 且9. 二次函数 的图象如图所示,对称轴为直线 ,下列结论错误的是( )
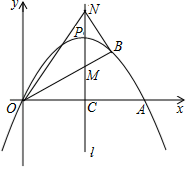
A、28 B、24 C、21 D、148. 关于x的方程 的解为正数,则k的取值范围是( )A、 B、 C、 且 D、 且9. 二次函数 的图象如图所示,对称轴为直线 ,下列结论错误的是( )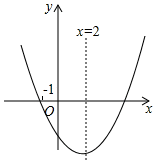 A、 B、当 时,顶点的坐标为 C、当 时, D、当 时,y随x的增大而增大10. 如图,四边形 是边长为1的正方形, 是等边三角形,连接 并延长交 的延长线于点H , 连接 交 于点Q , 下列结论:
A、 B、当 时,顶点的坐标为 C、当 时, D、当 时,y随x的增大而增大10. 如图,四边形 是边长为1的正方形, 是等边三角形,连接 并延长交 的延长线于点H , 连接 交 于点Q , 下列结论:① ;② ;③ ;④ .
其中符合题意的有( )
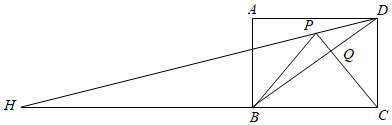 A、①②③ B、②③④ C、①③④ D、①②④
A、①②③ B、②③④ C、①③④ D、①②④二、填空题
-
11. 2018年10月24日,我国又一项世界级工程﹣﹣港珠澳大桥正式建成通车,它全长55000米,用科学记数法表示为米.12. 若一元二次方程 有两个不相等的实数根,则k的取值范围是 .13. 某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为分.14. 阅读材料:定义:如果一个数的平方等于 ,记为 ,这个数i叫做虚数单位,把形如 (a , b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算: ;
;
;
根据以上信息,完成下面计算:
.
15. 如图,在平面直角坐标系中,矩形 的顶点O落在坐标原点,点A、点C分别位于x轴,y轴的正半轴,G为线段 上一点,将 沿 翻折,O点恰好落在对角线 上的点P处,反比例函数 经过点B . 二次函数 的图象经过 、G、A三点,则该二次函数的解析式为 . (填一般式)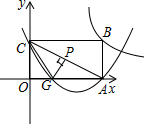
三、解答题
-
16. 计算:17. 解不等式组: ,把它的解集在数轴上表示出来,并写出其整数解.18. 先化简,再求值: ,其中a , b满足 .19. 如图,在四边形 中, ,延长 到E , 使 ,连接 交 于点F , 点F是 的中点.求证:
 (1)、 .(2)、四边形 是平行四边形.20. 汛期即将来临,为保证市民的生命和财产安全,市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡坡面从A至B共有30级阶梯,平均每级阶梯高30cm , 斜坡 的坡度 ;加固后,坝顶宽度增加2米,斜坡 的坡度 ,问工程完工后,共需土石多少立方米?(计算土石方时忽略阶梯,结果保留根号)
(1)、 .(2)、四边形 是平行四边形.20. 汛期即将来临,为保证市民的生命和财产安全,市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡坡面从A至B共有30级阶梯,平均每级阶梯高30cm , 斜坡 的坡度 ;加固后,坝顶宽度增加2米,斜坡 的坡度 ,问工程完工后,共需土石多少立方米?(计算土石方时忽略阶梯,结果保留根号) 21. 仙桃是遂宁市某地的特色时令水果.仙桃一上市,水果店的老板用2400元购进一批仙桃,很快售完;老板又用3700元购进第二批仙桃,所购件数是第一批的 倍,但进价比第一批每件多了5元.(1)、第一批仙桃每件进价是多少元?(2)、老板以每件225元的价格销售第二批仙桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于440元,剩余的仙桃每件售价至少打几折?(利润=售价﹣进价)22. 我市某校为了让学生的课余生活丰富多彩,开展了以下课外活动:
21. 仙桃是遂宁市某地的特色时令水果.仙桃一上市,水果店的老板用2400元购进一批仙桃,很快售完;老板又用3700元购进第二批仙桃,所购件数是第一批的 倍,但进价比第一批每件多了5元.(1)、第一批仙桃每件进价是多少元?(2)、老板以每件225元的价格销售第二批仙桃,售出80%后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于440元,剩余的仙桃每件售价至少打几折?(利润=售价﹣进价)22. 我市某校为了让学生的课余生活丰富多彩,开展了以下课外活动:代号
活动类型
A
经典诵读与写作
B
数学兴趣与培优
C
英语阅读与写作
D
艺体类
E
其他
为了解学生的选择情况,现从该校随机抽取了部分学生进行问卷调查(参与问卷调查的每名学生只能选择其中一项),并根据调查得到的数据绘制了如图所示的两幅不完整的统计图.请根据统计图提供的信息回答下列问题(要求写出简要的解答过程).
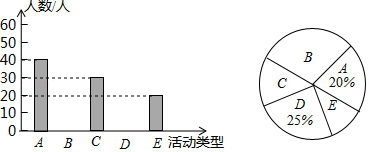 (1)、此次共调查了名学生.(2)、将条形统计图补充完整.(3)、“数学兴趣与培优”所在扇形的圆心角的度数为 .(4)、若该校共有2000名学生,请估计该校喜欢A、B、C三类活动的学生共有多少人?(5)、学校将从喜欢“A”类活动的学生中选取4位同学(其中女生2名,男生2名)参加校园“金话筒”朗诵初赛,并最终确定两名同学参加决赛,请用列表或画树状图的方法,求出刚好一男一女参加决赛的概率.23. 如图,一次函数 的图象与反比例函数 的图象交于点A与点 .
(1)、此次共调查了名学生.(2)、将条形统计图补充完整.(3)、“数学兴趣与培优”所在扇形的圆心角的度数为 .(4)、若该校共有2000名学生,请估计该校喜欢A、B、C三类活动的学生共有多少人?(5)、学校将从喜欢“A”类活动的学生中选取4位同学(其中女生2名,男生2名)参加校园“金话筒”朗诵初赛,并最终确定两名同学参加决赛,请用列表或画树状图的方法,求出刚好一男一女参加决赛的概率.23. 如图,一次函数 的图象与反比例函数 的图象交于点A与点 . (1)、求反比例函数的表达式;(2)、若动点P是第一象限内双曲线上的点(不与点A重合),连接 ,且过点P作y轴的平行线交直线 于点C , 连接 ,若 的面积为3,求出点P的坐标.
(1)、求反比例函数的表达式;(2)、若动点P是第一象限内双曲线上的点(不与点A重合),连接 ,且过点P作y轴的平行线交直线 于点C , 连接 ,若 的面积为3,求出点P的坐标.