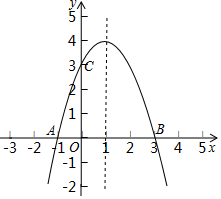四川省凉山州2019年中考数学试卷
试卷更新日期:2019-07-09 类型:中考真卷
一、单选题
-
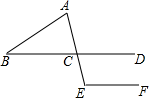
1. 的相反数是( )A、2 B、 C、 D、2. 2018年某州生产总值约为153300000000,用科学记数法表示数153300000000是( )A、 B、 C、 D、3. 如图, ,AE与BD交于点C, ,则 的度数为( )
 A、 B、 C、 D、4. 下列各式正确的是( )A、 B、 C、 D、5. 不等式 的解集是( )A、 B、 C、 D、6. 某班40名同学一周参加体育锻炼时间统计如表所示:
A、 B、 C、 D、4. 下列各式正确的是( )A、 B、 C、 D、5. 不等式 的解集是( )A、 B、 C、 D、6. 某班40名同学一周参加体育锻炼时间统计如表所示:人数(人)
3
17
13
7
时间(小时)
7
8
9
10
那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A、17,8.5 B、17,9 C、8,9 D、8,8.57. 下列命题:①直线外一点到这条直线的垂线段,叫做点到直线的距离;②两点之间线段最短;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.其中,真命题的个数是( )A、1 B、2 C、3 D、48. 如图,正比例函数 与反比例函数 的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连接BC,则 的面积等于( )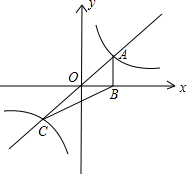 A、8 B、6 C、4 D、29. 如图,在 中, ,则 sinB 的值为( )
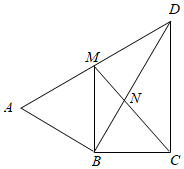
A、8 B、6 C、4 D、29. 如图,在 中, ,则 sinB 的值为( )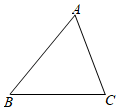 A、 B、 C、 D、10. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )
A、 B、 C、 D、10. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )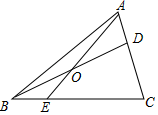 A、1:2 B、1:3 C、1:4 D、2:311. 如图,在 中, ,将△AOC绕点O顺时针旋转 后得到 ,则AC边在旋转过程中所扫过的图形的面积为( ) .
A、1:2 B、1:3 C、1:4 D、2:311. 如图,在 中, ,将△AOC绕点O顺时针旋转 后得到 ,则AC边在旋转过程中所扫过的图形的面积为( ) .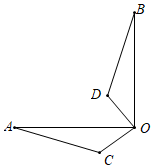 A、 B、 C、 D、12. 二次函数 的部分图象如图所示,有以下结论:① ;② ;③ ;④ ,其中错误结论的个数是( )
A、 B、 C、 D、12. 二次函数 的部分图象如图所示,有以下结论:① ;② ;③ ;④ ,其中错误结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 方程组 的解是 .14. 方程 的解是 .15. 如图所示,AB是⊙O的直径,弦 于H, ,则⊙O的半径是 .
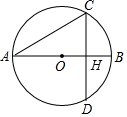 16. 在▱ABCD中,E是AD上一点,且点E将AD分为2:3的两部分,连接BE、AC相交于F,则 是 .17. 将抛物线 向左平移个单位后经过点 .18. 当 时,直线 与抛物线 有交点,则a的取值范围是 .19. 如图,正方形ABCD中, ,点P在BC上运动(不与B、C重合),过点P作 ,交CD于点Q,则CQ的最大值为 .
16. 在▱ABCD中,E是AD上一点,且点E将AD分为2:3的两部分,连接BE、AC相交于F,则 是 .17. 将抛物线 向左平移个单位后经过点 .18. 当 时,直线 与抛物线 有交点,则a的取值范围是 .19. 如图,正方形ABCD中, ,点P在BC上运动(不与B、C重合),过点P作 ,交CD于点Q,则CQ的最大值为 .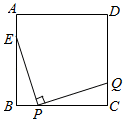
三、解答题
-
20. 计算: .21. 先化简,再求值: ,其中 .22. 如图,正方形ABCD的对角线AC、BD相交于点O,E是OC上一点,连接EB.过点A作 ,垂足为M,AM与BD相交于点F.求证: .
 23. 某校初中部举行诗词大会预选赛,学校对参赛同学获奖情况进行统计,绘制了如下两幅不完整的统计图.请结合图中相关数据解答下列问题:
23. 某校初中部举行诗词大会预选赛,学校对参赛同学获奖情况进行统计,绘制了如下两幅不完整的统计图.请结合图中相关数据解答下列问题: (1)、参加此次诗词大会预选赛的同学共有人;(2)、在扇形统计图中,“三等奖”所对应的扇形的圆心角的度数为;(3)、将条形统计图补充完整;(4)、若获得一等奖的同学中有 来自七年级, 来自九年级,其余的来自八年级,学校决定从获得一等奖的同学中任选两名同学参加全市诗词大会比赛,请通过列表或树状图方法求所选两名同学中,恰好是一名七年级和一名九年级同学的概率.24. 如图,点D是以AB为直径的⊙O上一点,过点B作⊙O的切线,交AD的延长线于点C,E是BC的中点,连接DE并延长与AB的延长线交于点F
(1)、参加此次诗词大会预选赛的同学共有人;(2)、在扇形统计图中,“三等奖”所对应的扇形的圆心角的度数为;(3)、将条形统计图补充完整;(4)、若获得一等奖的同学中有 来自七年级, 来自九年级,其余的来自八年级,学校决定从获得一等奖的同学中任选两名同学参加全市诗词大会比赛,请通过列表或树状图方法求所选两名同学中,恰好是一名七年级和一名九年级同学的概率.24. 如图,点D是以AB为直径的⊙O上一点,过点B作⊙O的切线,交AD的延长线于点C,E是BC的中点,连接DE并延长与AB的延长线交于点F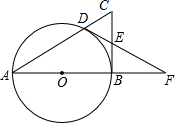 (1)、求证:DF是⊙O的切线;(2)、若 ,求AD的长.25. 已知二次函数 的图象与x轴交于 两点,且 ,求a的值.26. 根据有理数乘法(除法)法则可知:①若 (或 ),则 或 ;②若 (或 ),则 或 .
(1)、求证:DF是⊙O的切线;(2)、若 ,求AD的长.25. 已知二次函数 的图象与x轴交于 两点,且 ,求a的值.26. 根据有理数乘法(除法)法则可知:①若 (或 ),则 或 ;②若 (或 ),则 或 .根据上述知识,求不等式 的解集:
解:原不等式可化为:(1) 或(2) .
由(1)得, ,由(2)得, ,
∴原不等式的解集为: 或
请你运用所学知识,结合上述材料解答下列问题:
(1)、不等式 的解集为 .(2)、求不等式 的解集(要求写出解答过程)