四川省广安市中考2019年数学试卷

试卷更新日期：2019-07-09 类型：中考真卷

进入出卷网下载

一、填空题

1. 点 $M (x ﹣ 1 ， ﹣ 3)$ 在第四象限，则x的取值范围是．

查看试题解析
2. 因式分解： $3 a^{4} - 3 b^{4} =$ ．

查看试题解析
3. 等腰三角形的两边长分别为 $6 c m ， 13 c m$ ，其周长为cm．

查看试题解析
4. 如图，正五边形ABCDE中，对角线AC与BE相交于点F，则 $∠ A F E =$ 度．

查看试题解析
5. 在某市中考体考前，某初三学生对自己某次实心球训练的录像进行分析，发现实心球飞行高度y（米）与水平距离x（米）之间的关系为 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，由此可知该生此次实心球训练的成绩为米．

查看试题解析
6. 如图，在平面直角坐标系中，点 $A_{1}$ 的坐标为 $(1 ， 0)$ ，以 $O A_{1}$ 为直角边作 $R t Δ O A_{1} A_{2}$ ，并使 $∠ A_{1} O A_{2} ＝ 60 °$ ，再以 $O A_{2}$ 为直角边作 $R t Δ O A_{2} A_{3}$ ，并使 $∠ A_{2} O A_{3} ＝ 60 °$ ，再以 $O A_{3}$ 为直角边作 $R t Δ O A_{3} A_{4}$ ，并使 $∠ A_{3} O A_{4} ＝ 60 °$ …按此规律进行下去，则点 $A_{2019}$ 的坐标为．

查看试题解析

二、解答题

7. 计算： ${(- 1)}^{4} - | 1 - \sqrt{3} | + 6 \tan 30^{°} - {(3 - \sqrt{27})}^{2}$

查看试题解析
8. 解分式方程： $\frac{x}{x - 2} - 1 = \frac{4}{x^{2} - 4 x + 4}$ ．

查看试题解析
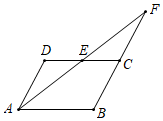
9. 如图，点E是▱ABCD的CD边的中点，AE、BC的延长线交于点F， $C F = 3 ， C E = 2$ ，求▱ABCD的周长．

查看试题解析
10. 如图，已知 $A (n ， ﹣ 2) ， B (- 1 ， 4)$ 是一次函数 $y = k x + b$ 和反比例函数 $y = \frac{m}{x}$ 的图象的两个交点．

(1)、求反比例函数和一次函数的解析式；

(2)、求△AOB的面积．

查看试题解析
11. 为了提高学生的阅读能力，我市某校开展了“读好书，助成长”的活动，并计划购置一批图书，购书前，对学生喜欢阅读的图书类型进行了抽样调查，并将调查数据绘制成两幅不完整的统计图，如图所示，请根据统计图回答下列问题：

(1)、本次调查共抽取了名学生，两幅统计图中的m＝， n＝．

(2)、已知该校共有3600名学生，请你估计该校喜欢阅读“A”类图书的学生约有多少人？

(3)、学校将举办读书知识竞赛，九年级1班要在本班3名优胜者（2男1女）中随机选送2人参赛，请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率．

查看试题解析
12. 为了节能减排，我市某校准备购买某种品牌的节能灯，已知3只A型节能灯和5只B型节能灯共需50元，2只A型节能灯和3只B型节能灯共需31元．

(1)、求1只A型节能灯和1只B型节能灯的售价各是多少元？

(2)、学校准备购买这两种型号的节能灯共200只，要求A型节能灯的数量不超过B型节能灯的数量的3倍，请设计出最省钱的购买方案，并说明理由．

查看试题解析
13. 如图，某数学兴趣小组为测量一颗古树BH和教学楼CG的高，先在A处用高1.5米的测角仪AF测得古树顶端H的仰角 $∠ H F E$ 为 $45 °$ ，此时教学楼顶端G恰好在视线FH上，再向前走10米到达B处，又测得教学楼顶端G的仰角 $∠ G E D$ 为 $60 °$ ，点A、B、C三点在同一水平线上．

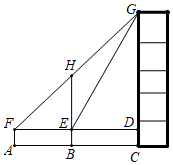(1)、求古树BH的高；

(2)、求教学楼CG的高．（参考数据： $\sqrt{2} = 1.4 ， \sqrt{3} = 1.7$ ）

查看试题解析
14. 在数学活动课上，王老师要求学生将图1所示的3×3正方形方格纸，剪掉其中两个方格，使之成为轴对称图形．规定：凡通过旋转能重合的图形视为同一种图形，如图2的四幅图就视为同一种设计方案（阴影部分为要剪掉部分）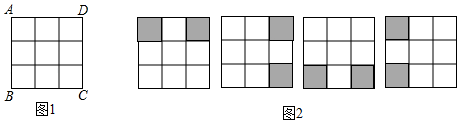

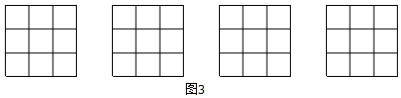
请在图中画出4种不同的设计方案，将每种方案中要剪掉的两个方格涂黑（每个3×3的正方形方格画一种，例图除外）

查看试题解析
15. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 ° ， A C = 6 ， B C = 8$ ，AD平分 $∠ B A C$ ，AD交BC于点D， $E D ⊥ A D$ 交AB于点E， $Δ A D E$ 的外接圆⊙O交AC于点F，连接EF．

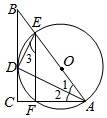(1)、求证：BC是⊙O的切线；

(2)、求⊙O的半径r及 $∠ 3$ 的正切值．

查看试题解析
16. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴交于A、B两点（A在B的左侧），与y轴交于点N，过A点的直线l： $y = k x + n$ 与y轴交于点C，与抛物线 $y = - x^{2} + b x + c$ 的另一个交点为D，已知 $A (- 1 ， 0) ， D (5 ， - 6)$ ，P点为抛物线 $y = ﹣ x^{2} + b x + c$ 上一动点（不与A、D重合）．

(1)、求抛物线和直线l的解析式；

(2)、当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作 $P F / / y$ 轴交直线l于点F，求 $P E + P F$ 的最大值；

(3)、设M为直线l上的点，探究是否存在点M，使得以点N、C，M、P为顶点的四边形为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．

查看试题解析